Difference between revisions of "Extrapolation"
From MohidWiki
| Line 2: | Line 2: | ||
==Weighted Average== | ==Weighted Average== | ||
| − | Suppose you have a discrete dataset <math>I</math>, with coordinates <math>X</math> on a normed space, <math>d\left(\ | + | Suppose you have a discrete dataset <math>I</math>, with coordinates <math>X</math> on a normed space, <math>d\left(.\,,\,.\right)</math>, and want to map the dataset to another dataset, <math>O</math>, with a new set of coordinates <math>Y</math>. The operation is performed by constructing mapping coefficients <math>w</math>, also called "weights", and by performing a linear combination of the elements of <math>I</math> with the weights, <math>w</math>, to compute each element of <math>O</math>. |
<math>O_k = \frac{ \sum_i w_{ki} \, I_i }{\sum_i w_{ki}}; </math> | <math>O_k = \frac{ \sum_i w_{ki} \, I_i }{\sum_i w_{ki}}; </math> | ||
Revision as of 10:41, 10 February 2012
Extrapolation is often required when interpolation techniques cannot be used; often when mapping information from one dataset to a grid. Extrapolation methods vary, yielding different results both in quality and in performance. This article proposes a couple of simple extrapolation techniques that use all the information available to extrapolate. The techniques inspire from the weighted average principle.
Contents
Weighted Average
Suppose you have a discrete dataset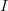 
, with coordinates 
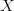on a normed space, 
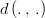, and want to map the dataset to another dataset, 
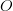, with a new set of coordinates 
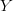. The operation is performed by constructing mapping coefficients 
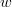, also called "weights", and by performing a linear combination of the elements of 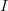with the weights, 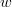, to compute each element of .
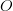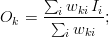
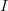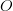Any method of constructing the weights is valid and depends on the nature of the mapping. A practical use-case consists in performing an interpolation/extrapolation of the data from to and thus the weights 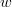are usually a function of the coordinates 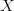and 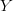and of the norm of the space. More complex techniques could be used, with 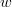also as a function of 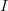and its derivatives, but these will not be considered in this text.
