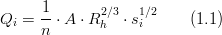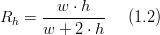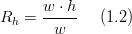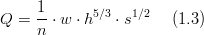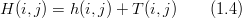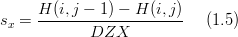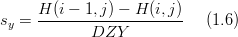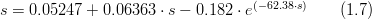Personal tools

Difference between revisions of "Module Runoff"

From MohidWiki

Jump to: navigation, search
(→‎References)
(→‎Manning Equation)
 
(48 intermediate revisions by 4 users not shown)
Line 1: Line 1:
 
==Overview==
 
==Overview==
−
Module Runoff allows the calculation of the overland surface runoff over a regular structured grid as function of the water column and terrain slope. The water column, namely the water located above the terrain, is given by the [[Module Basin]] where the precipitation is converting into a water column considering the losses due to the evapotranspiration and the infiltration processes. In particular the overland flow is evaluated by the Manning’s equation <ref name="Miller2005p23" />.
+
Module Runoff allows the calculation of the overland surface runoff over a grid as function of the water column slopes between adjacen cells (dynamic wave). The water column, namely the water located above the terrain, is given by the [[Module Basin]] after considering the precipitation input and the losses due to the evaporation and the infiltration.  
  
 
==Main Processes==
 
==Main Processes==
 +
The ModuleRunoff computes flow at cell faces using three different approaches (user option)
 +
#Full St. Venant Equation in 2D (shallow water equations)
 +
#Manning Equation with surface water gradient (diffuse wave)
 +
#Manning Equation with bottom gradient (kinematic wave)
 +
 +
===St. Venant Equations ===
 +
The St. Venant Equations are derived from the Newton's second law taking into account inertia effects. In this case a 2D approach is followed. [[Equations_in_Mohid_Land#2D_descritization_.28Runoff.29 | See equations description]].
 +
 
===Manning Equation===
 
===Manning Equation===
  
−
The overland surface runoff is calculated at the interface of the grid cells and it is obtained by applying the Manning's equation:
+
The overland surface runoff flow (m3/s) is calculated at the cell faces and it can be obtained by applying the Manning's equation.
 +
In this case inertia effects are neglected and forces balance bottom friction.
  
−
:<math>Q=\frac{1}{n}\cdot A\cdot R_{h}^{2/3}\cdot s^{1/2}\hspace {5.7cm}(1.1)</math>  
+
<ref>Gauckler, P. (1867), Etudes Théoriques et Pratiques sur l'Ecoulement et le Mouvement des Eaux, Comptes Rendues de l'Académie des Sciences, Paris, France, Tome 64, pp. 818–822</ref> :
 +
 
 +
:<math>Q_i=\frac{1}{n}\cdot A\cdot R_{h}^{2/3}\cdot s_i^{1/2}\,\,\,\,\,\,\,\,\,\,\,\,(1.1)</math>  
  
 
where:
 
where:
 
:{|
 
:{|
−
| ''Q'' || is the overland flow (m<sup>3</sup>/s)
+
| ''Qi'' || is the overland flow in each direction (m<sup>3</sup>/s)
 
|-
 
|-
 
| ''A'' || is the area of the cross-section (m<sup>2</sup>)
 
| ''A'' || is the area of the cross-section (m<sup>2</sup>)
Line 19: Line 30:
 
| ''R<sub>h</sub>''|| is the hydraulic radius (m)
 
| ''R<sub>h</sub>''|| is the hydraulic radius (m)
 
|-
 
|-
−
| ''S'' || is the slope of the water surface  (m/m)  
+
| ''Si'' || is the slope of the water surface  (m/m)  
 
|}
 
|}
  
  
−
In order to apply the Manning's equation each grid cell is considered as an open channel as shown in the scheme below.
+
====Hydraulic radius====
  
−
[[Image:Figure00.jpg|thumb|center|upright=8.0|Figure 1: Cell scheme]]
+
In rectangular channels, the hydraulic radius is evaluated by the formula:
  
−
where:
 
−
:{|
 
−
| ''h'' || is the water column (m)
 
−
|-
 
−
| ''w'' || is the cell width (m)
 
−
|}
 
−
 
−
===Hydraulics radius===
 
  
−
The hydraulic radius is evaluated by the formula:
+
:<math>R_{h}=\frac{w\cdot h}{w+2\cdot h}\,\,\,\,\,\,\,\,(1.2)</math> 
  
 +
But in runoff the lateral cell face is open boundary (to the next cell) not exerting friction in a surface as the bottom boundary, and so hydraulic radius can be rewritten:
  
−
:<math>\[R_{h}=\frac{w\cdot h}{w+2\cdot h}\hspace {6.8cm}(1.2)</math> 
 
  
 +
:<math>R_{h}=\frac{w\cdot h}{w}\,\,\,\,\,\,\,\,(1.2)</math>
  
−
In according with the Figure 1  the width is 'much' grater than the water column (w>>h) and the hydraulic radius can be considered only R<sub>h</sub>=h. Therefore the Manning's equation can be simplified as:
 
  
 +
and the hydraulic radius is R<sub>h</sub>=h. Therefore the Manning's equation can be rewritten as:
  
  
−
:<math>\[Q=\frac{1}{n}\cdot w\cdot h^{5/3}\cdot s^{1/2}\hspace {5.8cm}(1.3)</math>
+
:<math>Q=\frac{1}{n}\cdot w\cdot h^{5/3}\cdot s^{1/2}\,\,\,\,\,\,\,\,(1.3)</math>
  
−
===Slope===
+
====Slope====
  
−
The slope (s) is calculated by the difference of the water levels at the extremities of the considered cell:
+
The slope (s) is calculated by the difference of the water levels (H) at the extremities of the considered cell:
 
   
 
   
  
−
:<math>\[H(i,j)=\h(i,j)+T(i,j)\hspace {5.5cm}(1.4)</math>   
+
:<math>H(i,j)= h(i,j)+T(i,j)\,\,\,\,\,\,\,\,\,\,\,\,(1.4)</math>   
  
  
Line 71: Line 75:
  
  
−
:<math>\[s_{x}=\frac{H(i,j-1)-H(i,j)}{DZX}\hspace {5.1cm}(1.5)</math>   
+
:<math>s_{x}=\frac{H(i,j-1)-H(i,j)}{DZX}\,\,\,\,\,\,\,\,(1.5)</math>   
  
  
Line 87: Line 91:
  
  
−
:<math>\[s_{y}=\frac{H(i-1,j)-H(i,j)}{DZY}\hspace {5.1cm}(1.6)</math>   
+
:<math>s_{y}=\frac{H(i-1,j)-H(i,j)}{DZY}\,\,\,\,\,\,\,\,(1.6)</math>   
  
  
Line 101: Line 105:
 
|}
 
|}
  
−
In order to take in account the limitation given by the Manning's equation (1.1)[it tends to overestimate the flow velocity when solpe > 0.04] , the slope value obtained by the formulas (1.5) and (1.6) it  is subsequently adjusted by the following function:
+
In order to take in account the limitation given by the Manning's equation (1.1) that tends to overestimate the flow velocity when solpe > 0.04, the slope value obtained by the formulas (1.5) and (1.6) it  is subsequently adjusted by the following function:
 +
[http://www.hkh-friend.net.np/rhdc/training/lectures/HEGGEN/Tc_3.pdf Slope correction given by City of Albuquerque, 1997, p.22-26]
  
  
−
:<math>s= 0.05247 + 0.06363 \cdot s - 0.182\cdot e^{(-62.38\cdot s)}\hspace {2.4cm}(1.7)</math>
+
 
 +
:<math>s= 0.05247 + 0.06363 \cdot s - 0.182\cdot e^{(-62.38\cdot s)}\,\,\,\,\,\,\,\,\,\,\,\,(1.7)</math>
  
  
Line 114: Line 120:
 
===Manning cofficient===
 
===Manning cofficient===
  
−
The Manning coefficient is derived from the land use map. Indeed by using a GIS program it is possible to associate at each cell a land use class in order to obtain by the support of an abacus a Manning coefficent value.
+
The Manning coefficient is derived from the land use map. Indeed by using a GIS program it is possible to associate at each cell a land use class in order to obtain, by the support of an abacus or table, a Manning coefficent value. See the Other Features section.
  
−
===Calculated Flows===
+
===Connection with River===
  
−
The flows obtained by the formula [3] are diveded into flows in X direction and Y direction according with the Figure 2.
 
  
−
 
+
In the eventuality presence of a river it is possible to obtain two different configurations:
−
[[Image:Figure02.jpg|thumb|center|upright=2.0|Figure 2:Flow directions]]
 
−
 
 
−
 
 
−
In the eventuality presence of a river in the basin analyzed it is possible to obtain two different configurations:
 
  
 
:{|
 
:{|
Line 138: Line 139:
 
|-
 
|-
 
[[Image:Figure04.jpg|thumb|center|upright=2|Figure 4: Flow from the river]]
 
[[Image:Figure04.jpg|thumb|center|upright=2|Figure 4: Flow from the river]]
 +
 +
 +
The flow between river and runoff is computed using the same formulation as in runoff cells using the surface gradient between runoff and river.
  
 
|}
 
|}
 +
 +
==Boundary Conditions==
 +
In Runoff there is the option to define the boundary condition as a level or as a timeserie (tide). This level will be imposed at the boundary and if the user wishes a) the water will only exit if the water level is higher than the boundary level and no inflow is allowed or b) inflow is allowed if the boundary level is higher than water level.
 +
 +
===Computation===
 +
Boundary fluxes are computed after the flow computation iteration.
 +
 +
The boundary flux is computed with celerity in both directions (x and y) where boundary face exists.
 +
Qi = - cel  *  Li * min(dh,h)
 +
 +
where cel is celerity = SQRT(g * h)
 +
where Li is cell length perpendicular to direction
 +
where dh is level difference, if negative, boundary level is higher than runoff level
 +
where h is water height
 +
 +
 +
the water height in celerity is water column (maximum column between inside and outside) and height for Area is the minimum between the difference between levels (dh) and the water column (if boundary level higher, height is dh, otherwise is also dh except if boundary level is lower than topography and in that case the minimum is the water column).
 +
 +
===Keywords===
 +
The keyword in Runoff_X.dat that connects the open boundary is:
 +
IMPOSE_BOUNDARY_VALUE    : 1
 +
 +
The keyword that defines the boundary level is:
 +
BOUNDARY_VALUE            : 100.
 +
 +
The open boundary computation can be limited to specific areas defining the maximum altimetry that the boundary will be open. This is specifically useful when one wants to open the surface water at flat areas where in fact the flux can go trough the boundaries of the watershed delimitation.
 +
MAX_DTM_FOR_BOUNDARY      : 1000.
 +
 +
Using a value of the latter keyword higher than the maximum altimetry found in the watershed will make the boundary open in all watershed.
 +
 +
 +
To allow water to flow in if the boundary level is higher use this keyword connected. Otherwise the boundary level will behave as a wall that if boundary level is higher than it does not allow water to exit but dos not also allow it to enter.
 +
ALLOW_BOUNDARY_INFLOW    : 1
 +
 +
If the user wants to use a timeserie for imposing level (tide) than use this block where Piezometer6.dat is a time serie with level in time in the second column that the user will impose.
 +
<begin_boundary>
 +
FILENAME                  : ..\General Data\Boundary Conditions\Piezometer6.dat
 +
DATA_COLUMN              : 2
 +
<end_boundary>
 +
 +
==Discharges==
 +
 +
In Runoff the discharges may be positive or negative (Runoff uses discharge flow) and are dealt with ModuleDischarges.
 +
 +
===Computation===
 +
The discharges are initialized in Construct phase reading its locations and checking if inside boundaries.
 +
 +
In Modification phase, the several discharges flows are accounted and water volume updated. The computation is inside the water column iteration process.
 +
And integration variable integrates this flow for RunoffProperties.
 +
 +
===Keywords===
 +
For discharges to be read in Discharges_X.dat the following keyword needs to exist in the Runoff_X.dat
 +
DISCHARGES : 1
 +
Without these keyword no matter what is inside Discharges_X.dat it will not be read!
 +
  
 
==Other Features==
 
==Other Features==
Line 164: Line 223:
 
  <EndOverLandCoefficient>
 
  <EndOverLandCoefficient>
  
−
==Outputs==
+
== Outputs==
  
−
==References==
+
== References ==
−
<references/>
+
* Hubert Chanson|Chanson, H. (2004), The Hydraulics of Open Channel Flow, Butterworth-Heinemann, Oxford, UK, 2nd edition, 630 pages
 +
*http://www.hkh-friend.net.np/rhdc/training/lectures/HEGGEN/Tc_3.pdf
  
 
==Data File ==
 
==Data File ==

Latest revision as of 16:02, 18 May 2017

Overview

Module Runoff allows the calculation of the overland surface runoff over a grid as function of the water column slopes between adjacen cells (dynamic wave). The water column, namely the water located above the terrain, is given by the Module Basin after considering the precipitation input and the losses due to the evaporation and the infiltration.

Main Processes

The ModuleRunoff computes flow at cell faces using three different approaches (user option)

  1. Full St. Venant Equation in 2D (shallow water equations)
  2. Manning Equation with surface water gradient (diffuse wave)
  3. Manning Equation with bottom gradient (kinematic wave)

St. Venant Equations

The St. Venant Equations are derived from the Newton's second law taking into account inertia effects. In this case a 2D approach is followed. See equations description.

Manning Equation

The overland surface runoff flow (m3/s) is calculated at the cell faces and it can be obtained by applying the Manning's equation. In this case inertia effects are neglected and forces balance bottom friction.

<ref>Gauckler, P. (1867), Etudes Théoriques et Pratiques sur l'Ecoulement et le Mouvement des Eaux, Comptes Rendues de l'Académie des Sciences, Paris, France, Tome 64, pp. 818–822</ref> :

Q_i=\frac{1}{n}\cdot A\cdot R_{h}^{2/3}\cdot s_i^{1/2}\,\,\,\,\,\,\,\,\,\,\,\,(1.1)

where:

Qi is the overland flow in each direction (m3/s)
A is the area of the cross-section (m2)
n is the Manning coefficient (s/m1/3)
Rh is the hydraulic radius (m)
Si is the slope of the water surface (m/m)


Hydraulic radius

In rectangular channels, the hydraulic radius is evaluated by the formula:


R_{h}=\frac{w\cdot h}{w+2\cdot h}\,\,\,\,\,\,\,\,(1.2)

But in runoff the lateral cell face is open boundary (to the next cell) not exerting friction in a surface as the bottom boundary, and so hydraulic radius can be rewritten:


R_{h}=\frac{w\cdot h}{w}\,\,\,\,\,\,\,\,(1.2)


and the hydraulic radius is Rh=h. Therefore the Manning's equation can be rewritten as:


Q=\frac{1}{n}\cdot w\cdot h^{5/3}\cdot s^{1/2}\,\,\,\,\,\,\,\,(1.3)

Slope

The slope (s) is calculated by the difference of the water levels (H) at the extremities of the considered cell:


H(i,j)= h(i,j)+T(i,j)\,\,\,\,\,\,\,\,\,\,\,\,(1.4)


where:

H is the water level (m)
h(i,j) is the water column (m)
T(i,j) is the Topography (m)
j is X direction
i is Y direction


s_{x}=\frac{H(i,j-1)-H(i,j)}{DZX}\,\,\,\,\,\,\,\,(1.5)


where:

sx is the slope in the X direction (m)
H(i,j-1) is the water column at the left face of the cell (m)
H(i,j) is the water column at the right face of the cell (m)
DZX is width of the cell in the X direction (m)


s_{y}=\frac{H(i-1,j)-H(i,j)}{DZY}\,\,\,\,\,\,\,\,(1.6)


where:

sy is the slope in the Y direction (m)
H(i-1,j) is the water column at the left face of the cell (m)
H(i,j) is the water column at the right face of the cell (m)
DZY is width of the cell in the X direction (m)

In order to take in account the limitation given by the Manning's equation (1.1) that tends to overestimate the flow velocity when solpe > 0.04, the slope value obtained by the formulas (1.5) and (1.6) it is subsequently adjusted by the following function: Slope correction given by City of Albuquerque, 1997, p.22-26


s= 0.05247 + 0.06363 \cdot s - 0.182\cdot e^{(-62.38\cdot s)}\,\,\,\,\,\,\,\,\,\,\,\,(1.7)


where:

s is the slope (m)

Manning cofficient

The Manning coefficient is derived from the land use map. Indeed by using a GIS program it is possible to associate at each cell a land use class in order to obtain, by the support of an abacus or table, a Manning coefficent value. See the Other Features section.

Connection with River

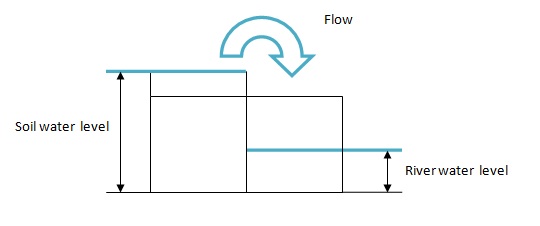
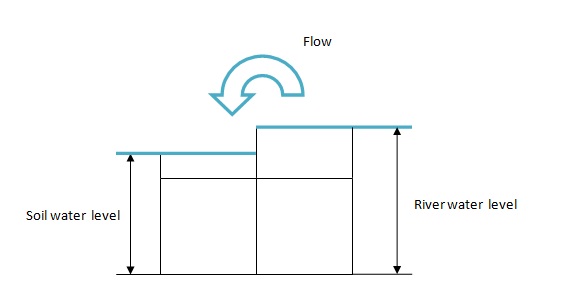
In the eventuality presence of a river it is possible to obtain two different configurations:

  • Flow to the river when the water level of the river is lower that soil one
Figure 3: Flow to the river


  • Flow from the river when the water level is higher than the soil one


Figure 4: Flow from the river


The flow between river and runoff is computed using the same formulation as in runoff cells using the surface gradient between runoff and river.

Boundary Conditions

In Runoff there is the option to define the boundary condition as a level or as a timeserie (tide). This level will be imposed at the boundary and if the user wishes a) the water will only exit if the water level is higher than the boundary level and no inflow is allowed or b) inflow is allowed if the boundary level is higher than water level.

Computation

Boundary fluxes are computed after the flow computation iteration.

The boundary flux is computed with celerity in both directions (x and y) where boundary face exists. 

Qi = - cel  *  Li * min(dh,h)

where cel is celerity = SQRT(g * h) where Li is cell length perpendicular to direction where dh is level difference, if negative, boundary level is higher than runoff level where h is water height


the water height in celerity is water column (maximum column between inside and outside) and height for Area is the minimum between the difference between levels (dh) and the water column (if boundary level higher, height is dh, otherwise is also dh except if boundary level is lower than topography and in that case the minimum is the water column).

Keywords

The keyword in Runoff_X.dat that connects the open boundary is: 

IMPOSE_BOUNDARY_VALUE     : 1

The keyword that defines the boundary level is: 

BOUNDARY_VALUE            : 100.

The open boundary computation can be limited to specific areas defining the maximum altimetry that the boundary will be open. This is specifically useful when one wants to open the surface water at flat areas where in fact the flux can go trough the boundaries of the watershed delimitation. 

MAX_DTM_FOR_BOUNDARY      : 1000.

Using a value of the latter keyword higher than the maximum altimetry found in the watershed will make the boundary open in all watershed.


To allow water to flow in if the boundary level is higher use this keyword connected. Otherwise the boundary level will behave as a wall that if boundary level is higher than it does not allow water to exit but dos not also allow it to enter. 

ALLOW_BOUNDARY_INFLOW     : 1

If the user wants to use a timeserie for imposing level (tide) than use this block where Piezometer6.dat is a time serie with level in time in the second column that the user will impose. 

<begin_boundary>
FILENAME                  : ..\General Data\Boundary Conditions\Piezometer6.dat
DATA_COLUMN               : 2
<end_boundary>

Discharges

In Runoff the discharges may be positive or negative (Runoff uses discharge flow) and are dealt with ModuleDischarges.

Computation

The discharges are initialized in Construct phase reading its locations and checking if inside boundaries.

In Modification phase, the several discharges flows are accounted and water volume updated. The computation is inside the water column iteration process. And integration variable integrates this flow for RunoffProperties.

Keywords

For discharges to be read in Discharges_X.dat the following keyword needs to exist in the Runoff_X.dat 

DISCHARGES : 1

Without these keyword no matter what is inside Discharges_X.dat it will not be read!


Other Features

How To Generate Manning Coefficients

Manning coefficients must be provided in runoff data file.

Options:

  • Use a constant value
  • Define a Manning's grid: One possible option is to associate Manning with land use classes (shape file). In this case can use MOHID GIS going to menu [Tools] \Longrightarrow [Shape to Grid Data] and provide:
(i) the grid (model grid)
ii) the land use shape file
iii) the corespondence between land use codes and Manning

Use Manning inicialization with Module FillMatrix standards in the block: 

<BeginOverLandCoefficient>
FILE_IN_TIME           : NONE
INITIALIZATION_METHOD  : ASCII_FILE
REMAIN_CONSTANT        : 1
DEFAULTVALUE           : 0.08
FILENAME               : ..\..\GeneralData\Runoff\Mannings200m_v2.dat 
<EndOverLandCoefficient>

Outputs

References

Data File

Keywords

Sample

Retrieved from "http://wiki.mohid.com/index.php?title=Module_Runoff&oldid=7621"