Difference between revisions of "Module Waves"
From MohidWiki
(→SWAN based example) |
|||
| Line 137: | Line 137: | ||
=== SWAN based example === | === SWAN based example === | ||
| − | This example MOHID input data files shows how to read wave forcing from an hdf5, generated from the results of a wave model, one such as [[SWAN | + | This example MOHID input data files shows how to read wave forcing from an hdf5, generated from the results of a wave model, one such as [[Mohid_Swan|SWAN]]. Go check out the [[Mohid_Swan|SWAN]] wiki to configure and run the [[Mohid_Swan|SWAN]] for your domain... |
Hydrodynamic_x.dat | Hydrodynamic_x.dat | ||
Revision as of 10:56, 16 June 2011
Contents
Overview
Module Waves is responsible to simulate surface waves in MOHID. It can act as a wave database, reading wave data from files, or it can predict wave parameters through a surface wave generation model which is responsible for computing surface wave properties and its related parameters, therefore communicating directly with the water-air interface module, responsible for all the fluxes between the water column and the atmosphere. The water-air interface module provides wind velocity, direction and shear stresses, receiving from the surface wave module the necessary information to compute water surface rugosity, which can ultimately be used by the turbulence and hydrodynamic module. As surface waves depend and influence water elevations and currents, the wave module also communicates with the hydrodynamic module, providing it with radiation stresses and receiving water depths. Also wave parameters as orbital velocity and excursion are used by the sediment-water interface module to compute bottom shear stresses, which will be used both in hydrodynamics and in sediment transport, controlling erosion and deposition processes.
Fetch-based wave generation model
The surface wave generation model predicts significant wave height and wave period at the end of generation zone based on fetch, water depth and wind speed and direction. The model is restricted to surface wave generation by local wind and propagation is not considered explicitly. As a consequence, this model can only be applied to areas where wave propagation from the exterior is limited (e.g. ocean swell). Examples of such areas are coastal lagoons, lakes or estuaries with limited wave interaction with the ocean.
Algorithm
In areas where the fetch is not restricted (e.g. open sea), there is a dominant fetch and small changes in wind direction don’t significantly change fetch length or the direction of the generated wave. On the other hand, for wind directions parallel to the shore and mainly for lakes, lagoons or estuaries, a small variation in the wind direction can generate significant changes in the wind’s length of action. In these areas there is not a predominant direction for fetch. In order to calculate the effective fetch it is then necessary to take into account the local morphology of the study area considering several directions, each one with a different weight. Thus, for the same wind direction, a point with more obstacles in the near directions has assigned a smaller fetch than a point with more water length in the same directions. These distances are then used to calculate the effective fetch on each cell, in only 8 cardinal directions. Thus, this calculus is only made once, having each cell 8 values of effective fetch. The result is stored in memory during the entire simulation. During the simulation period, in each time step and in each and every cell, depending on wind direction, the effective fetch is selected from the list of 8 values, and it’s used together with wind speed and water depth to calculate the wave parameters. There are some limitations computing effective fetch when simulating domains with large open boundaries, because there is no information to evaluate fetch distances in the boundaries when wind is blowing from the exterior. Effective fetch is computed considering the highest water level in the simulation domain. This means that when if there are areas that during the simulation become uncovered (e.g. forming a temporary tidal flat island), effective fetch is not adjusted. In those cells, all calculus is switched off until they are flooded again.
Equations
Wind Velocity Dependent Wave Model
This approach has applicability mainly in open deep water where wave conditions are not depth and fetch limited.
The Wave Height and Wave Period can be empirically determined as function of wind speed, according to ADIOS model formulations (NOAA, 1994).
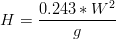
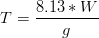
Where H is Wave Height (m), T is Wave Period (s), W is the wind velocity (m/s) and g the gravity acceleration (m/s2).
Wind Velocity, Depth and Fetch Dependent Wave Model
As propagation is not considered, the model does not require any initial conditions and there's no time dependency in the wave parameters evolution. Thus, significant wave height and mean wave period can be computed directly, being only required to provide the necessary input variables: wind speed, water depth and fetch. The equations were adapted from the CE-QUAL-W2 model (Cole, 2003) and were previously developed by Seymour (1977) and Kang (1982).
Failed to parse (Cannot write to or create math temp directory): Hs=\frac{W^2}g0.283\tanh\left[0.53\left(\frac{gH}{W^2}}\right)^{0.75}\right]\tanh\left[\frac{0.0125\left(\frac{gF}{W^2}\right)^{0.42}}{\tanh\left[0.53\left(\frac{gH}{W^2}\right)^{0.75}\right]}\right]
Failed to parse (Cannot write to or create math temp directory): Ts=\frac{2piW}g1.2\tanh\left[0.833\left(\frac{gH}{W^2}}\right)^{0.375}\right]\tanh\left[\frac{0.077\left(\frac{gF}{W^2}\right)^{0.25}}{\tanh\left[0.833\left(\frac{gH}{W^2}\right)^{0.375}\right]}\right]
Where, Hs is Significant Wave Height, Ts is Significant Wave Period, W is the wind velocity modulus (m/s), H the water depth (m) and F, the fetch distance (m).
These equations predict wave height and wave period at the end of the generation zone, therefore the duration of the wind action it is not accounted for, because it is admitted that the total development of the waves is achieved. The hyperbolic function in eq. 1 and eq. 2 simulates the effects that, for high depths, waves are not influenced by the bottom and is also used to avoid the indefinite increasing of wave height and wave period with increasing fetch. A multiplicative factor for both wave height and period are included in the equations (unitary default value) enabling the calibration of the model results against available waves data.
The broader equation (eq. 3 and Figure 4) for effective fetch (Fe) was obtained from Rogala (1997) and Howes (1997):
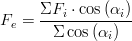
Figure 5. Fetch calculation with 3 and 5 directions.
Where Fi is the fetch distance (m) in the i direction and αi = angle (º) between the wind direction and the i direction. For the fetch directions, 3 or 5 distances (eq. 4 and eq. 5 respectively) can be used (Figure 5). This is called the effective modified fetch (Fm):
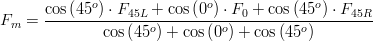
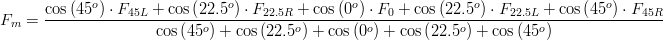
Where, F45L and F22L are the distances to land in the directions 22.5º and 45º left of the wind direction (m); F45R and F22R are the distances to land in the directions 22.5º and 45º right of the wind direction (m); and F0 is distance to land along wind direction (m). The weight given to each distance is based on the cosine function, taking a unitary weight for the wind direction and decreasing weights to angles away from this direction. In order to compute the effective fetch, distances to land need to be computed. As described above the distances can be computed in two different ways: i) in a grid-based method with an algorithm that moves in the grid along the 8 or 16 directions until it finds a land cell or the end of the grid; ii) in a “graphical” method that computes distances between cell centre and land polygons.
Wave orbital velocity and excursion
Linear wave theory is generally applied to determine the near-bed velocities. In case of symmetrical (sinusoidal) small-amplitude waves in relatively deep waters this theory yields good results. When waves approach shallower waters, the waves will be distorted leading to asymmetrical wave profiles and higher order wave theories are necessary to determine the near-bed velocities. In this model only linear wave theory is considered, therefore applying it, the peak value of the orbital excursion (Aδ) and velocity (Uδ) at the edge of the wave boundary layer can be expressed as:
User manual
Main options
In this chapter it is briefly described how to use Module Waves. The different options provided by the module can be defined through an input data file, similarly to other modules in MOHID. In order to couple this module with the rest of the model simulation, it has to be activated in the Module Model input data file, by defining the following keyword:
WAVES : 1
ModuleWaves can be used as a database, reading the solution for the different parameters (radiation stresses, significant wave height, mean wave period and mean wave direction) from a file, or it can be used to compute wave parameters based on external information. Depending on the options chosen, ModuleWaves might be dependent on the activation of other modules, namely the Atmosphere and InterfaceWaterAir modules, which provide wind information. In order to use the wave module so that it influences hydrodynamics (water level and currents), the user must activate the radiation stress options and activate in the Hydrodynamic input data file the following keyword:
WAVESTRESS : 1
To use Module Waves so that the waves effect contributes to the calculation of bottom shear stress it is necessary to turn on the following keyword and block in InterfaceSedimentWater data file:
WAVETENSION : 1
<begin_waverugosity> INITIALIZATION_METHOD : CONSTANT FILE_IN_TIME : NONE DEFAULTVALUE : 9e-3 REMAIN_CONSTANT : 0 <end_waverugosity>
This will also enable to consider waves influence on resuspension and deposition of particulate matter in the water-sediment interface.
Input data file
In a simulation, it is possible to choose between the calculation of wave height and wave period as described in point 2.2.1 (simpler) and as in point 2.2.2 (fetch and depth dependent). This is made by a keyword named [WAVEGEN_TYPE] (keyword = 0 and the method is the one in 2.2.1 and keyword = 1 stands for method in 2.2.2; by default the value is 0 (zero)).
The working scheme of the model is very simple: in the constructing phase of MOHID, the distances to land are calculated for all water cells in the 8 or 16 cardinal directions defined by the keyword [WINDROSE_DIRECTIONS].
The distances to land can be computed with two different methods, distinguishing them with the keyword [DISTANCE_TO_LAND_METHOD]. If this keyword equals zero, the distances to land are computed along the grid, incrementing half cell size in each cycle step, until land or end of grid is encountered. If the keyword equals one, distances are computed performing tangents to the points and intersecting them with polygons (Land Areas) segments. The first method can not be used with nested models (if grid ends before directions reaches land).
Fetch based example
Fetch, is only calculated once in the simulation (in the MOHID construction phase).
OUTPUT_TIME : 0 86400
RADIATION_TENSION_X : 0
RADIATION_TENSION_Y : 0
WAVE_PERIOD : 1
WAVE_HEIGHT : 1
WAVE_DIRECTION : 1
WAVEGEN_TYPE : 1
DISTANCE_TO_LAND_METHOD : 0
WINDROSE_DIRECTIONS : 16
WAVE_HEIGHT_PARAMETER : 1.
WAVE_PERIOD_PARAMETER : 1.
<begin_landareafiles>
Polygon.xy
<end_landareafiles>
<begin_waveperiod>
INITIALIZATION_METHOD : CONSTANT
DEFAULTVALUE : 12.
REMAIN_CONSTANT : 0
OUTPUT_HDF : 1
TIME_SERIE : 1
<end_waveperiod>
<begin_waveheight>
INITIALIZATION_METHOD : CONSTANT
DEFAULTVALUE : 0.1
REMAIN_CONSTANT : 0
OUTPUT_HDF : 1
TIME_SERIE : 1
<end_waveheight>
<begin_wavedirection>
INITIALIZATION_METHOD : CONSTANT
DEFAULTVALUE : 0.
REMAIN_CONSTANT : 0
OUTPUT_HDF : 1
TIME_SERIE : 1
<end_wavedirection>
SWAN based example
This example MOHID input data files shows how to read wave forcing from an hdf5, generated from the results of a wave model, one such as SWAN. Go check out the SWAN wiki to configure and run the SWAN for your domain...
Hydrodynamic_x.dat WAVE_STRESS : 1
InterfaceSedimentWater_x.dat <begin_waverugosity> FILE_IN_TIME : NONE REMAIN_CONSTANT : 0 OUTPUT_HDF : 1 TIME_SERIE : 0 DEFAULTVALUE : 0.0025 <end_waverugosity> WAVETENSION : 1
Waves_x.dat WAVE_PERIOD : 1 WAVE_DIRECTION : 1 WAVE_HEIGHT : 1 RADIATION_TENSION_X : 1 RADIATION_TENSION_Y : 1 <begin_waveheight> NAME : significant wave height UNITS : m DESCRIPTION : wave height variable INITIALIZATION_METHOD : HDF FILE_IN_TIME : HDF FILENAME : Waves.hdf5 DEFAULTVALUE : 0.0 OUTPUT_HDF : 1 <end_waveheight> <begin_wavedirection> NAME : mean wave direction UNITS : º DESCRIPTION : mean wave direction INITIALIZATION_METHOD : HDF FILE_IN_TIME : HDF FILENAME : Waves.hdf5 DEFAULTVALUE : 0.0 OUTPUT_HDF : 1 <end_wavedirection> <begin_waveperiod> NAME : mean wave period UNITS : s DESCRIPTION : mean wave period WW3 INITIALIZATION_METHOD : HDF FILE_IN_TIME : HDF FILENAME : Waves.hdf5 DEFAULTVALUE : 0.0 OUTPUT_HDF : 1 <end_waveperiod> <begin_radiationstress_x> NAME : wave stress X UNITS : Pa DESCRIPTION : /wave stress X INITIALIZATION_METHOD : HDF FILE_IN_TIME : HDF FILENAME : Waves.hdf5 DEFAULTVALUE : 0.0 OUTPUT_HDF : 1 <end_radiationstress_x> <begin_radiationstress_y> NAME : wave stress Y UNITS : Pa DESCRIPTION : /wave stress Y INITIALIZATION_METHOD : HDF FILE_IN_TIME : HDF FILENAME : Waves.hdf5 DEFAULTVALUE : 0.0 OUTPUT_HDF : 1 <end_radiationstress_y>
Outputs
Time series
Maps (HDF5 format)
References
- Braunschweig F, Leitao PC, Fernandes L, Pina P, Neves RJJ. The object oriented design of the integrated Water Modelling System. Developments in Water Science. 2004;55:1079-1090. Available at: http://dx.doi.org/10.1016/S0167-5648(04)80126-6.
- Cole, T.M. and S.A. Wells, 2003. CE-QUAL-W2: A two-dimensional, laterally averaged, Hydrodynamic and Water Quality Model, Version 3.2. Instruction Report EL-03-1, US Army Engineering and Research Development Center, Vicksburg, MS.
- Howes, 1997. British Columbia Estuary mapping Systems – Appendix A: Wave Exposure Calculation. Ministry of Sustainable Resource Management, British Columbia U.S.A.
- NOAA (1994) - ADIOSTM (Automated Data Inquiry for Oil Spills) user’s manual. Seattle: Hazardous Materials Response and Assessment Division, NOAA. Prepared for the U.S. Coast Guard Research and Development Center, Groton Connecticut, 50 pp.
- Rogala, J.T., 1997. Estimating Fetch for Navigation Pools in the Upper Mississippi River Using a Geographic Information System. United States Geological Survey -Project Status Report 97-08 .
- Seymour, R.J., 1977. Estimating Wave Generation in Restricted Fetches. J. ASME WW2, May 1977 pp251-263.