Difference between revisions of "Extrapolation"
From MohidWiki
| Line 1: | Line 1: | ||
| − | Extrapolation is often required when interpolation techniques cannot be used; often when mapping information from one dataset to a grid. Extrapolation methods vary, yielding different results both in quality and in performance. This article proposes a couple of simple extrapolation | + | Extrapolation is often required when interpolation techniques cannot be used; often when mapping information from one dataset to a grid. Extrapolation methods vary, yielding different results both in quality and in performance. This article proposes a couple of simple extrapolation techniques that use all the information available to extrapolate. The techniques inspire from the weighted average principle. |
==Weighted Average== | ==Weighted Average== | ||
Revision as of 10:33, 10 February 2012
Extrapolation is often required when interpolation techniques cannot be used; often when mapping information from one dataset to a grid. Extrapolation methods vary, yielding different results both in quality and in performance. This article proposes a couple of simple extrapolation techniques that use all the information available to extrapolate. The techniques inspire from the weighted average principle.
Contents
Weighted Average
Suppose you have a discrete dataset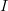 
, with coordinates 
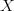on a normed space, and want to map the dataset to another dataset, 
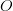, with a new set of coordinates 
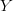. The operation is performed by constructing mapping coefficients 
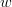, also called "weights", and by performing a linear combination of the elements of 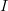with the weights, 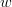, to compute each element of .
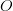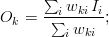
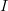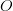Any method of constructing the weights is valid and depends on the nature of the mapping. A practical use-case consists in performing an interpolation/extrapolation of the data from to and thus the weights 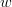are a function of the coordinates 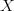and 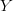and of the norm of the space.
