Difference between revisions of "VARIABLEDT"
From MohidWiki
| Line 42: | Line 42: | ||
<math> \Delta t = \min_{p\;ijk} \left( \frac{ m }{ \Phi } \right) \quad\;\;\;\; \text{if}\quad\;\;\Phi \gt 0</math>. | <math> \Delta t = \min_{p\;ijk} \left( \frac{ m }{ \Phi } \right) \quad\;\;\;\; \text{if}\quad\;\;\Phi \gt 0</math>. | ||
| − | where <math>m</math> and <math>\Phi</math> are, respectively, the mass (<math>kg\,m^{-3}</math>) and the massic flow (<math>kg\,m^{-3}\,s^{-1}</math>) of the property <math>p</math> at the cell indexed by <math>i,\,j,\,k</math>. | + | where <math>m</math> and <math>\Phi</math> are, respectively, the mass (<math>kg\,m^{-3}</math>) and the net massic flow (<math>kg\,m^{-3}\,s^{-1}</math>) of the property <math>p</math> at the cell indexed by <math>i,\,j,\,k</math>. |
This takes into account only advective and diffusive fluxes but disregards sources and sink terms. For momentum, it also disregards the time-step constraints imposed by the gravity surface wave mode or any other physical process occuring at scales below ten times the computed <math> \Delta t </math>. | This takes into account only advective and diffusive fluxes but disregards sources and sink terms. For momentum, it also disregards the time-step constraints imposed by the gravity surface wave mode or any other physical process occuring at scales below ten times the computed <math> \Delta t </math>. | ||
Latest revision as of 19:28, 15 February 2012
User's manual
To activate a variable time step bounded between a minimum and maximum DT, in configuration file Model_x.dat
VARIABLEDT : 1 DT : 10. MAXDT : 100.
A log file DTLog.txt is stored in the results folder /res of the main domain if the option DT_LOG is set in the nomfich.dat file in /exe folder of the main domain. Such a log file is useful to trace which cell of which property is the weakest link that could generate an instability.
DT_LOG : ..\res\DT_Log_2.log
An option can be checked in MOHID Studio or MOHID GUI that enables the logging of variable time steps.
An excerpt of a log file looks like this (Iterartion number, dt, i, j, k, model name, property name):
1, DT: 10.000, I: 177, J: 75, K: 43, Model - Property: Portugal - momentum
2, DT: 10.000, I: 37, J: 1, K: 43, Model - Property: Portugal - momentum
3, DT: 10.000, I: 177, J: 101, K: 43, Model - Property: Portugal - momentum
4, DT: 10.000, I: 62, J: 1, K: 43, Model - Property: Portugal - momentum
5, DT: 10.000, I: 156, J: 93, K: 25, Model - Property: Portugal - nitrate
6, DT: 10.000, I: 69, J: 1, K: 43, Model - Property: Portugal - momentum
7, DT: 10.000, I: 177, J: 84, K: 43, Model - Property: Portugal - momentum
8, DT: 10.000, I: 64, J: 1, K: 43, Model - Property: Portugal - momentum
9, DT: 12.000, I: 155, J: 106, K: 33, Model - Property: Portugal - nitrate
10, DT: 13.846, I: 65, J: 1, K: 49, Model - Property: Portugal - nitrate
11, DT: 16.364, I: 25, J: 4, K: 45, Model - Property: Portugal - nitrate
12, DT: 18.000, I: 32, J: 6, K: 43, Model - Property: Portugal - nitrate
13, DT: 20.000, I: 26, J: 6, K: 44, Model - Property: Portugal - nitrate
14, DT: 22.500, I: 27, J: 8, K: 44, Model - Property: Portugal - nitrate
15, DT: 25.714, I: 156, J: 119, K: 30, Model - Property: Portugal - nitrate
16, DT: 30.000, I: 32, J: 4, K: 42, Model - Property: Portugal - silicate acid
17, DT: 36.000, I: 30, J: 3, K: 42, Model - Property: Portugal - silicate acid
18, DT: 36.000, I: 27, J: 10, K: 44, Model - Property: Portugal - nitrate
19, DT: 36.000, I: 32, J: 6, K: 43, Model - Property: Portugal - silicate acid
20, DT: 36.000, I: 30, J: 5, K: 42, Model - Property: Portugal - silicate acid
Physical rationale
The main idea to compute an ideal time-step is to choose the largest time-step above which the numerical model iteration would overshoot. This is equivalent to making sure that no cell in any property can deplete more than its property mass in one time-step, given that it has a net flux with positive divergence. Mathematically speaking this would be equivalent to:
Failed to parse (unknown error): \Delta t = \min_{p\;ijk} \left( \frac{ m }{ \Phi } \right) \quad\;\;\;\; \text{if}\quad\;\;\Phi \gt 0 .
where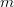 
and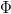 
are, respectively, the mass (
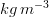) and the net massic flow (
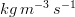) of the property 
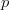at the cell indexed by 
.
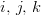This takes into account only advective and diffusive fluxes but disregards sources and sink terms. For momentum, it also disregards the time-step constraints imposed by the gravity surface wave mode or any other physical process occuring at scales below ten times the computed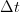 
.
