Module Hydrodynamic

Overview

The hydrodynamic model solves the primitive continuity and momentum equations for the surface elevation and 3D velocity field for incompressible flows, in orthogonal horizontal coordinates and generic vertical coordinates, assuming hydrostatic equilibrium and Boussinesq approximations.

Density is computed depending on salt, temperature and pressure, by the UNESCO equation of state (UNESCO, 1981). The model uses an ADI (Alternate Direction Implicit) time discretization scheme which minimizes stability restrictions, and is defined in an Arakawa-C type grid. In the bottom, shear stress can be computed with the assumption of a logarithmic velocity gradient:

In the free surface, a momentum flux can also be imposed in the form of shear stress.

Momentum, mass and heat transport is computed using a generic 3D advection-diffusion library including various advection schemes namely: first, second and third order upwind, centred differences and TVD (Total Variation Diminishing). Advection is solved in the three directions as a one-dimensional case and various time discretizations can be combined: explicit, semi-implicit or fully implicit.

Boundary conditions

Bottom

In the bottom, advective fluxes are imposed as null and diffusive flux of momentum is estimated by means of a bottom stress that is calculated by a non-slip method with a quadratic law that depends on the near-bottom velocity. So, the diffusive term at the bottom is written as:

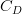$C_{D}$ is the bottom drag coefficient that is calculated with the expression:

where 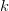$k$ is von Karman constant and 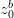$z^{b}_{0}$ is the bottom roughness length. This quadratic law is derived from the logarithmic law of the wall near boundaries characteristic of boundary layers, as the bottom velocities are located half a grid box above the bottom. This term is calculated semi-implicitly following Backhaus (1985) for numerical stability reasons.

Surface

Momentum

Diffusive flux of momentum is imposed explicitly by means of a wind surface stress, 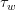$\tau_{ w}$:

Mass

A water flux can be imposed (e.g. precipitation or evaporation) or computed (e.g. evaporation) at the surface of the water column.

Open boundaries

The open boundaries have two main components: Component 1 - condition assumed in the open boundary of the horizontal spatial derivatives of each evolution equation (momentum, mass/heat); Component 2 - nugding assumed in the domain cells adjacent to to the open boundary for each property.

Component 1: sea level: In the case of sea level (or water level). The availabe conditions are clamped (RADIATION : 0) or radiative off the type Falther (1974) (RADIATION : 2) horizontal velocity : clamped (null value or interpolated from the above nested level) or null gradient. There is also an hybrid approach where one of the two option already presented are assume for the barotropic component and radiative condition is assumed for the baroclinic component. This is described in detail below; water properties (eg. salinity, temperature) : clamped (value prescribed by the user or value interpolated from a higher nested level) or null gradient

Component 2: horizontal velocity : can be added in any model cell an aceleration term (u ref - u)/Trelax (sink/source of momentum). Where u ref is the velocity of the exterior solution and u the velocity computed by the model and Trelax in the relxation time scale. By default is assumed an exponetial evolution of the relxation time scale with a minimum value of ~1day in the open boundary and ~10.000 days 20 cells away from the open boundary. The u ref can be autonumous solution like a ocean operational solution (eg. Mercator Ocean or Hycom-US) or can be a higher nested level). water properties (eg. salinity, temperature) : the same methodology as the one described for the velocity is followed.

Exterior solution

The exterior solution can be imposed using three different ways. 1 - file : this is off-line definition of the exterior solution. It is used to define an exterior solution based in external data sources other models or solutions based in field data (eg. Levitus); 2 - nesting : this the on-line way to define an exterior solution. This done running several nesting levels and the higher levels are interpolated automaticly to the lower ones; 3 - tidal gauges: this is specific of the sea level and is used to impose the sea level along the open boundary based in the definition of the sea level is several localized points. The sea level in each point can be defined using a time serie or tidal harmonics.

The options to define the exterior solution via file (option 1) are described in detail in Module_FillMatrix#Overview .

Baroclinic radiation

In the baroclinic radiation boundary condition the options available are related with the way the internal celerity is computed. The available options are: 1 – Orlansky: celerity computed based in orlanski method (very noisy in schematic and realistic conditions) 2 – Constant: constant celerity estimated by the user (good performance in schematic cases, creates sporadically discontinuities); 3 – Oey&Chen: empiric celerity proposed by Oey and Chen c = sqrt(1e-3*g*H)

The experience has shown that with the present MOHID open boundary conditions the baroclinic radiation reveal in realistic forcing conditions to be irrelevant and some times create discontinuities in the open boundary.

Moving boundaries (Drying and flooding)

Moving boundaries are closed boundaries that change position in time. If there are intertidal zones in the domain, some points can be alternatively covered or uncovered depending on tidal elevation. A stable algorithm is required for modeling these zones and their effect on hydrodynamics of estuaries.

Land boundaries

In these boundaries the domain is limited by land. For the resolution used, this lateral boundary layer is resolved, so a impermeable, free slip condition can be used:

$\frac{{\partial \overrightarrow{{v_H }} }} {{\partial \eta }} = 0$

$\overrightarrow{v} \cdot \overrightarrow{n} = 0$

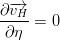
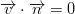
In the finite volume formalism, these conditions are implemented straightforwardly by specifying zero normal water fluxes and zero momentum diffusive fluxes at the cell faces in contact with land.

A non-slipling condition can also be used in lateral land boundaries.

Discharges

See Module Discharges.

Other features

Data assimilation

See Relaxation and Module Assimilation.

Outputs

Maps (HDF5 format)

To write 3D results use keyword OUTPUT_TIME and define keyword:

OUTPUT_HDF           : 1

in each property that you whish to write results.

To write results only in the surface use keyword SURFACE_OUTPUT_TIME and define keyword:

OUTPUT_SURFACE_HDF   : 1

in each property that you which to write results. Surface results can be written with a different frequency than the normal 3D maps.