Module Hydrodynamic

Overview

The hydrodynamic model solves the primitive continuity and momentum equations for the surface elevation and 3D velocity field for incompressible flows, in orthogonal horizontal coordinates and generic vertical coordinates, assuming hydrostatic equilibrium and Boussinesq approximations.

Density is computed depending on salt, temperature and pressure, by the UNESCO equation of state (UNESCO, 1981). The model uses an ADI (Alternate Direction Implicit) time discretization scheme which minimizes stability restrictions, and is defined in an Arakawa-C type grid. In the bottom, shear stress can be computed with the assumption of a logarithmic velocity gradient:

In the free surface, a momentum flux can also be imposed in the form of shear stress.

Momentum, mass and heat transport is computed using a generic 3D advection-diffusion library including various advection schemes namely: first, second and third order upwind, centred differences and TVD (Total Variation Diminishing). Advection is solved in the three directions as a one-dimensional case and various time discretizations can be combined: explicit, semi-implicit or fully implicit.

Boundary conditions

Bottom

In the bottom, advective fluxes are imposed as null and diffusive flux of momentum is estimated by means of a bottom stress that is calculated by a non-slip method with a quadratic law that depends on the near-bottom velocity. So, the diffusive term at the bottom is written as:

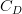$C_{D}$ is the bottom drag coefficient that is calculated with the expression:

where 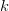$k$ is von Karman constant and 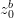$z^{b}_{0}$ is the bottom roughness length. This quadratic law is derived from the logarithmic law of the wall near boundaries characteristic of boundary layers, as the bottom velocities are located half a grid box above the bottom. This term is calculated semi-implicitly following Backhaus (1985) for numerical stability reasons.

Surface

Momentum

Diffusive flux of momentum is imposed explicitly by means of a wind surface stress, 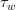$\tau_{ w}$:

Mass

A water flux can be imposed (e.g. precipitation or evaporation) or computed (e.g. evaporation) at the surface of the water column.

Open boundaries

Main components

The MOHID methodology to impose the open boundary conditions have two main components:

Component 1 - open boundary condition of the horizontal spatial derivatives of the momentum, mass and heat evolution equations;

Component 2 - nugding (or relaxation) assumed in the domain cells adjacent to to the open boundary for each property.

Component 1: sea level: In the case of sea level (or water level). The availabe conditions are clamped (RADIATION : 0) or radiative condition of the type Flather (1974) (RADIATION : 2) (u -u ref)= sqrt(u*H) * (n -n ref). Where u ref is the velocity component of the exterior solution normal to the open boundary and u the velocity computed by the model with the same direction of u ref, n ref is the sea level of the exterior solution and n is the sea level computed by the model and H is the water column computed by the model (H = n + h) where h is the bathymetry depth. horizontal velocity : clamped (null value or interpolated from the above nested level) or null gradient. There is also an hybrid approach where one of the two option already presented are assume for the barotropic component and radiative condition is assumed for the baroclinic component. This is described in detail below; water properties (eg. salinity, temperature) : clamped (value prescribed by the user or value interpolated from a higher nested level) or null gradient

Component 2: horizontal velocity : can be added in any model cell an aceleration term (u ref - u)/Trelax (sink/source of momentum). Where u ref is the velocity of the exterior solution and u the velocity computed by the model and Trelax in the relxation time scale. By default is assumed an exponetial evolution of the relxation time scale with a minimum value of ~1day in the open boundary and ~10.000 days 20 cells away from the open boundary. The u ref can be autonomous solution like a ocean operational solution (eg. Mercator Ocean or Hycom-US) or can be a higher nested level). water properties (eg. salinity, temperature) : the same methodology as the one described for the velocity is followed.

Overall methodology

The idea is to try to have a relaxation time scale small enough to let information go in and at the same time high enough to let go the high frequency processes generate inside the model domain.

Usually the user wants to impose information with a sub-inertial frequency (or low frequency - time scale above the inertial time scale ) in the open boundary. The information generate inside the domain not present in the exterior solution can be consider mainly high frequency (above the inertial frequency). The general idea is using the relaxation (or nudging) to "impose" the exterior solution and absorbed the signature of the high frequency processes (generate inside the model domain) in the water properties that propagate slowly (celerity of internal waves O(1 m/s))) and radiate the sea level high frequency processes that propagate very fast (celerity O(100 m/s) at 1000 m depth).

Exterior solution

The exterior solution can be imposed using three different ways. 1 - file : this is off-line definition of the exterior solution. It is used to define an exterior solution based in external data sources other models or solutions based in field data (eg. Levitus); 2 - nesting : this the on-line way to define an exterior solution. This done running several nesting levels and the higher levels are interpolated automaticly to the lower ones; 3 - tidal gauges: this is specific of the sea level and is used to impose the sea level along the open boundary based in the definition of the sea level is several localized points. The sea level in each point can be defined using a time serie or tidal harmonics.

The options to define the exterior solution via file (option 1) are described in detail in Module_FillMatrix#Overview .

Baroclinic radiation

In the baroclinic radiation boundary condition the options available are related with the way the internal celerity is computed. The available options are: 1 – Orlansky: celerity computed based in orlanski method (very noisy in schematic and realistic conditions) 2 – Constant: constant celerity estimated by the user (good performance in schematic cases, creates sporadically discontinuities); 3 – Oey&Chen: empiric celerity proposed by Oey and Chen c = sqrt(1e-3*g*H)

The experience has shown that with the present MOHID open boundary conditions the baroclinic radiation reveal in realistic forcing conditions to be irrelevant and some times create discontinuities in the open boundary.

Definition examples

The MOHID model has a quite generic approach to the open boundary conditions definition. The number of examples is quite diverse. However, three main types are using in a more persistent way:

1 - Modelling the sea level evolution in a costal area: 
 a) clamped sea level;
 b) null gradient for the velocity;
 c)exterior solution : tidal gauges; 

2 - Downscale of a ocean operational solution (eg. Mercator Ocean or HYCOM-US):
 a)radiative (Flather, 1974) sea level;
 b)velocity/water properties null gradient + relaxation;
 c)exterior solution : ocean operational solution);

3 - communication between nested models 
 a)radiative (Flather, 1974) sea level;
 b)velocity/water properties clamped + relaxation;
 c)exterior solution : higher  nested level;

See examples Boundary conditions input examples

Moving boundaries (Drying and flooding)

Moving boundaries are closed boundaries that change position in time. If there are intertidal zones in the domain, some points can be alternatively covered or uncovered depending on tidal elevation. A stable algorithm is required for modeling these zones and their effect on hydrodynamics of estuaries.

Land boundaries

In these boundaries the domain is limited by land. For the resolution used, this lateral boundary layer is resolved, so a impermeable, free slip condition can be used:

$\frac{{\partial \overrightarrow{{v_H }} }} {{\partial \eta }} = 0$

$\overrightarrow{v} \cdot \overrightarrow{n} = 0$

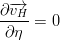
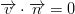
In the finite volume formalism, these conditions are implemented straightforwardly by specifying zero normal water fluxes and zero momentum diffusive fluxes at the cell faces in contact with land.

A non-slipling condition can also be used in lateral land boundaries.

Discharges

See Module Discharges.

Other features

Data assimilation

See Relaxation and Module Assimilation.

Submodel

To run a domain as a submodel the following logical keyword must be set to 1

SUBMODEL                     : 0/1 (Check if the user wants to run this model as a submodel)

Submodel hot start initialization when the initial values for the submodel comes from the father model values.

SUBMODEL_FATHER_HOT_START    : 0/1 (Check if the user wants to the submodel with a father hot start)
SUBMODEL_EXTRAPOLATE         : 0/1 (Hydrodynamic intial values are extrapolated from a father model)

Hydrodynamic Obstacle

In order to correct velocities due to the existence of an object, a drag coefficient linked to a polygon can be defined by using this keywords in the hydrodynamic file.

OBSTACLE                  : 0/1    (Check if the user wants to add an hydrodynamic obstacle)

<begin_dragcoef>
NAME                      : obstacle drag coefficient
DEFAULTVALUE              : 0.
TYPE_ZUV                  : z
FILE_IN_TIME              : NONE
REMAIN_CONSTANT           : 1
FILE_IN_TIME              : NONE
INITIALIZATION_METHOD     : BOXES
FILENAME                  : ...     (Location of the file where the obstacle boxes are defined)  
BOXES_VALUES              : real    (Drag coefficient value for the defined boxes per cell) ![1/m]   
<end_dragcoef>

The drag coefficient (Xd) is defined per cell

![1/m] = [-]*[m^2]/[m^3]

Xd = 0.5 * Cd * Area of Reference per Cell / Cell volume

Cd - dimensionless drag coefficient (see Drag coefficient - Wikipedia)

For the case of pillars that occupy the entire water column

Area of Reference per cell = D * HT * nº of pillars per cell

D - diameter of pillars

HT - water column of the cell

Cell Volume = HT * dx * dy

dx - cell spatial step in x

dy - cell spatial step in y

dx * dy = cell horizontal area

![1/m] = [-] * [m] / [m] / [m]

Xd = 0.5 * Cd * D * nº of pillars per cell / dx / dy

Choose from a table Cd correspondent to the Reynolds number and shape (in this case a cylinder) of interest.

Thin walls

The user can override the compute faces mapping. This override can be variable in time. To this override option was called thin walls effect. The options available are the follow

If the user wants to connect the thin walls effect

THIN_WALLS                     : 1

If the thin walls effect in variable in time

THIN_WALLS_VARIABLE            : 1

Time serie file where the time variability of the thin walls effect is define.

THIN_WALLS_TIME_SERIE          : ..\..\GeneralData\Gate\Gate.dat 

To avoid extreme velocities along the thin walls a limit is define for the water level gradient. If the thin walls effect block the flow the water level gradient can increase extremely. This limit is only consider when the velocity is being computed.

WATER_LEVEL_GRAD_LIMIT         : 0.001 

The idea is to compute the acceleration due to the water level gradient in the follow way

Water level gradient acceleration = -g*min ( dn/dx, WATER_LEVEL_GRAD_LIMIT)

Column in the time serie file where the flag open/close (0/1) in defined

TIME_FLAG_COLUMN               : 2  

Block of X faces close where the thin walls effect is considered

<begin_thinwalls_u>
i j k
…
<end_thinwalls_u>

Block of Y faces close where the thin walls effect is considered

<begin_thinwalls_v>
i j k
…
<end_thinwalls_v>

Block of Z faces close where the thin walls effec is considered

<begin_thinwalls_w>
i j k
…
<end_thinwalls_w>

Outputs

Time series

• Add the following lines to the hydrodynamic configuration file, then save and close

TIME_SERIE             : 1
TIME_SERIE_LOCATION    : D:\Users\Soussou\GeneralData\TimeSeries\StLouisTimeSeries.dat

• Here's a typical time series configuration file

File generated by Mohid GIS

DT_OUTPUT_TIME                :  600
MAX_BUFFER_SIZE               :  10000

Based on GridData file        : D:\Users\Soussou\GeneralData\kml2gis\cascais.dat

Based on XYZ file             : D:\Users\Soussou\GeneralData\kml2gis\cascais.xyz

<BeginTimeSerie>
NAME                          : Station_0
LOCALIZATION_I                :  65
LOCALIZATION_J                :  127
LOCALIZATION_K                :  1
CENTER_CELL_X                 : -9.31735
CENTER_CELL_Y                 :  38.67645
ORIGINAL_X                    : -9.317324
ORIGINAL_Y                    :  38.67641
<EndTimeSerie>

The output will be time series with extension ".srh" i.e. Station_0.srh

Maps (HDF5 format)

To write 3D results use keyword OUTPUT_TIME and define keyword:

OUTPUT_HDF           : 1

in each property that you whish to write results.

To write results only in the surface use keyword SURFACE_OUTPUT_TIME and define keyword:

OUTPUT_SURFACE_HDF   : 1

in each property that you which to write results. Surface results can be written with a different frequency than the normal 3D maps.

Window Area (HDF5 format)

When this block is present, a HDF5 output is created with a selected model results window at a certain time step, the output is found at the res folder with the name Hydrodynamic_wX.hdf5. X corresponds to the number of window ordered by the position at the file. Typically used for Imposed Solution evolution.

<beginoutput>
<<beginoutwindow>>
OUTPUT_TIME_W                : ... (output time in seconds. Typically 0 & time interval i.e. 0 900.)
KLB_KUB_W                    : K K (Minimum and maximum vertical layers)
ILB_IUB_W                    : Y Y (Minimum and maximum I grid values along the Y-axis)
JLB_JUB_W                    : X X (Minimum and maximum J grid values along the X-axis)
<<endoutwindow>>

<<beginoutwindow>>
....
....
<<endoutwindow>>
<endoutput>

Statistics

Assign the following keywords to the hydrodynamic data file:

STATISTICS               : 1 
STATISTICS_FILE          : .. location of the statistics configuration file

STATISTICS_2D            : 1 
STATISTICS_FILE_2D       : .. location of the 2D statistics configuration file

Configuration of the statistics configuration file is described in Module Statistics