Difference between revisions of "Module PorousMedia"

Revision as of 17:23, 14 October 2011

Overview

Module Porous Media is responsible for handling all water fluxes in soil. In particular the infiltration flow is obtained from the potential water column available for this process. The potential water column is given by the Module Basin (the module that handles interface between modules) as reported below:

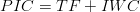
$PIC=TF+IWC$

where:

PIC	is the Potential Infiltration column (m)
TF	Throughfall is the percentage of the rain that reaches the soil (m)
IWC	is the Initial Water column (m)

The infiltration flux is calculated by the Buckingham-Darcy equation using head gradient between surface runoff and first soil layer (Jury et al,1991).

Main Processes

Porous Media Geometry

Porous Media is a 3D domain delimited in its upper limit by topography and lower limit by soil bottom (defined by user). In terms of soil definition it can be defined vertical horizons to link correspond to real soil horizons with different hydraulic carachteristics.

Water Flow

Soil contains a large distribution of pore sizes and channels through which water may flow. In general the water flow determination is based on the mass conservation and momentum equation. In the case of soil it is assumed that the forces of inertia are almost zero; therefore the balance is reduced to the forces of pressure, gravity and viscous. The equation that describes the flow through soil is the Buckingham Darcy equation (Jury et al,1991).

Failed to parse (Cannot write to or create math temp directory): v=-K\left ( \theta \right )\left ( \frac{\partial H}{\partial z} \right )=-K\left ( \theta \right )\left ( \frac{\partial h}{\partial z} + 1 \right )\,\,\,\,(1.1)\\

where:

v	is the water velocity at the cell interface (m/s)
H	is the hydraulic head (m)
θ	is the water content (m³/m³)
K	is the hydraulic conductivity (m/s)

The hydraulic head is given by the formula:

$H=h+p+z\,\,\,\,(1.2)$

where:

h	is the hydraulic head (m)
p	is hydrostatic pressure (m)
z	is the topography (m)

When in saturated conditions, hydraulic head is zero and hydrostatic pressure may occur (if water is at rest or decelerating). In unsaturated conditions hydrostatic pressure is zero and hydarulic head exists.

The soil is a very complex system, made up of a heterogeneous mixture of solid, liquid, and gaseous material. The liquid phase consists of soil water, which fills part or all of the open spaces between the soil particles. Therefore it is possible to divided the soil in two layers:

Saturated soil $\Longrightarrow$ The soil pores are filled by water

Unsaturated one $\Longrightarrow$ The soil pores are filled by water and air

In the first case the equation of Buckingham Darcy is simplified to the Darcy law and the parameter associated for its resolution are connected with the saturated layer. On the other hand for the resolution of the equation (1.1) a description of the characteristics of the the unsaturated layer is needed.

Vadose Zone

Many vadose flow and transport studies require description of unsaturated soil hydraulic proprieties over a wide range of pressure head. The hydraulic proprieties are described using the porous size distribution model of Maulem (1976) for hydraulic conductivity in combination with a water retention function introduced by Van Genuchten (1980).

Water content

Water content is the quantity of water contained in the soil (called soil moisture). It is given as a volumetric basis and it is defined mathematically as:

Failed to parse (Cannot write to or create math temp directory): \theta = \frac{V_w}{V_T}\hspace{5cm}(1.3)

Failed to parse (Cannot write to or create math temp directory): V_T = V_s + V_v = V_s + V_w + V_a\hspace{1.6cm}(1.4)

where:

$\theta$	is water content (m ³/m ³)
$V_w$	is the volume of water (m s³)
$V_T$	is the total volume (m ³)
$V_s$	is the soil volume (m ³)
$V_a$	is the air space (m ³)

Initial Condition

The user may define a water content initialization or choose the model to compute in the unsaturated area heads so that soil water is at Field Capacity. The below explains the latter.

Once determined the aquifer level (water table) the water content is associated at each cells by the following criteria:

If the cell is located above the water table $\theta=\theta_{s}$

If the cell is located over the water table $\theta=\theta_{ns}$

where:

$\theta=\theta_{s}$	is the water content in the saturated soil (m³/m³)
$\theta=\theta_{ns}$	is the water content in the non saturated soil (m³/m³)

In order to calculate field capacity by the equation (1.7) the evaluation of the suction head is needed :

Failed to parse (Cannot write to or create math temp directory): h=-DWZ\cdot 0.5\hspace{2cm}for\,\, the\,\, cells\,\, immediately\,\, above\,\, the\,\, water\,\, table \hspace{5cm} (1.5)

Failed to parse (Cannot write to or create math temp directory): h=-(-DZZ-h)\hspace{1.5cm}for\,\, the\,\, other\,\, cells\hspace{9.75cm} (1.6)

Figure 1: Suction Head Calculation

As shown in the picture the suction head is calculated in order to maintain the same total head (H = z + p + h) in the cells in agreement with the field capacity definition.

Water retention

The model use for characterizing the shape of water retention curves is the van Genuchten model:

Failed to parse (Cannot write to or create math temp directory): \theta(h) = \theta_r + \frac{\theta_s - \theta_r}{\left[ 1+(\alpha |h|)^n \right]^{1-1/n}}\hspace{0.5cm}\Longrightarrow\hspace{0.5cm}h(\theta)=\left |\frac{(S_{E}^{-1/n}-1)^{1/n}}{\alpha} \right |\hspace{3cm}(1.7)

Failed to parse (Cannot write to or create math temp directory): S_{E}=\frac{\theta-\theta_{r}}{\theta_{s}-\theta_{r}}\hspace{11cm}(1.8)

where:

$\theta(h)$	is the the water retention curve (m ³/m ³)
$\theta_s$	is the saturated water content (m ³/m ³)
$\theta_r$	is the residual water content (m ³/m ³)
h	is the suction head (m)
$\alpha$	is related to the inverse of the air entry (m _-1)
n	is a measure of the pore-size distribution n>1 (dimensionless)
$S_{E}$	is the effective saturation (dimensionless)

Saturated and Unsaturated Conductivity

The saturated conductivity is given depending on the type of soil; instead the unsaturated conductivity is obtained from the suction head by the Maulem model:

$K(\theta)=K_{s}\cdot Se^{L}\cdot (1-(1-Se^{1/m})^{m})^{2}$

where:

$K(\theta)$	is the unsaturated conductivity (m/s)
$K_{s}$	is the saturated conductivity(m/s)
L	empirical pore-connectivity (m)
m	m=1-1/n(dimensionless)

Evapotranspiration

Some water may be extracted from the soil because of the evaporation and transpiration processes, which become a sink in soil water profile. These two processes are currently named Evapotranspiration.

Potential Evapotranspiration may be modeled using the Penmann Monteith equation. Also, if vegetation exists, a differentiation between Potential Transpiration and Potential Evaporation is done using LAI. These computation are made in Module Basin since this is the module that handles water fluxes in the interface betwen modules.

However, not all of the potential water that can be evaporated or transpired will be in fact removed from the soil. The water that will really leave the soil through these processes is calculated: i) if vegetation exists, effective transpiration is computed in module Vegetation; ii) effective evaporation is computed in the Porous Media module. In Figure below it can be seen that the actual transpiration and evaporation are then used in Porous Media module to compute the new water content. The actual evaporation, which happens only at the soil surface, is calculated based on: i) a pressure head limit or ii) a soil conductivity limit, chosen by the user. It allows the model not to evaporate any surface water, even if it is available, when the soil head gets below the assigned value (i) or limits evaporation velocity to layer unsaturated conductivity (ii).

Evapotranspiration fluxogram in Mohid Land model

Remind that Feddes is one option for computing effective transpiration in plants in module Vegetation.

Iteration Process

Once obtained the water fluxes a balance on the water volume of each cell is apply in order to obtain the new water content $\theta$ . The balance applied is the following:

Horizontal Direction X

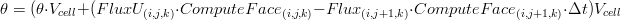
$\theta=(\theta\cdot V_{cell}+(FluxU_{(i,j,k)}\cdot ComputeFace_{(i,j,k)}-Flux_{(i,j+1,k)}\cdot ComputeFace_{(i,j+1,k)}\cdot \Delta t) V_{cell}$

Horizontal Direction Y

$\theta=(\theta\cdot V_{cell}+(FluxV_{(i,j,k)}\cdot ComputeFace_{(i,j,k)}-FluxV_{(i+1,j,k)}\cdot ComputeFace_{(i+1,j,k)})\cdot \Delta t)\cdot V_{cell}$

Vertical Direction W

$\theta=(\theta\cdot V_{cell}+(FluxW_{(i,j,k)}\cdot ComputeFace_{(i,j,k})-FluxW_{(i,j,k+1)}\cdot ComputeFace_{(i,j,k+1}))\cdot \Delta t)\cdot V_{cell}$

Transpiration Flux

$\theta=(\theta\cdot V_{cell}-(TranspFlux_{(i,j,k)}\Delta t)\cdot V_{cell}$

Evaporation Flux

$\theta=(\theta\cdot V_{cell}-(EvapFlux_{(i,j,k)}\Delta t)\cdot V_{cell}$

Infiltration Flux

$\theta=(\theta\cdot V_{cell}-(UnsatK\cdot Area_{cell}\cdot(1-Imp) \Delta t)\cdot V_{cell}$

where:

$\theta$	is the water content (m ³/m ³)
$V_{cell}$	is the cell volume (m ³)
$Area_{cell}$	is the cell area (m ²)
ComputeFace	is the computed face (dimensionless)
$\Delta t$	is the time step (s)
FluxX	is the flux in X direction (m ³/s)
FluxV	is the flux in Y direction (m ³/s)
FluxW	is the flux in W direction (m ³/s)
TranspFlux	is the transpiration flux (m ³/s)
EvapFlux	is the evaporation flux (m ³/s)
UnsatK	is unsaturated conductivity (m /s)
Imp	is the percentage of impermeable soil of the cell (dimensionless)

The value of $\theta$ so obtained is compared with one used in the volumes calculation and the iterative process stop when:

Failed to parse (Cannot write to or create math temp directory): (\theta^{'})-(\theta^{new})<\,\, Tolerance\hspace{3cm} (1.9)

where:

$\theta^{'}$

is the water content of the previous iteration (m ³/m ³)

If the equation (1.9) is not satisfy the temporal step is divided in half and the new value of $\theta$ is used for solving the equation (1.7) for restarting the calculation process. The iteration process is stoped when the tolerance desired is reached.

Figure 2: Time step reduction

Other Features

How to Generate Info needed in Porous Media

SoilMap

Model needs to know soil ID in each cell and layer to pick hydraulic properties from that type of soil.

Options:

Constant value
Soil Grid. One possible option is to associate with soil shape file. In this case can use MOHID GIS going to menu [Tools]->[Shape to Grid Data] and provide: i) the grid (model grid), ii) the soil shape file and iii) the corespondence between soil codes and soil ID defined in data file.

Soil ID must be defined in Module FillMatrix standards for each soil horizon defined (grid example):

<beginhorizon>
KLB                       : 1
KUB                       : 10

<beginproperty>
NAME                      : SoilID
DEFAULTVALUE              : 1
INITIALIZATION_METHOD     : ASCII_FILE
REMAIN_CONSTANT           : 1
FILENAME                  : ..\..\GeneralData\PorousMedia\SoilID200m.dat
<endproperty>

<beginproperty>
<endproperty>
..
<endhorizon>

Remarks

All the soil ID's appearing in the soil grid(s) must be defined in the PorousMedia data file in terms of hydraulic properties:

<beginsoiltype>
ID                        : 1
THETA_S                   : 0.3859
THETA_R                   : 0.0476
N_FIT                     : 1.39
SAT_K                     : 3.5556e-6
ALPHA                     : 2.75
L_FIT                     : 0.50
<endsoiltype>

<beginsoiltype>
ID                        : 2
...
<endsoiltype>
...

Soil Bottom

The soil depth must be known by the model. This is computed by the model from terrain altitude (topography) and soil bottom altitude. As so, a soil bottom grid is needed.

Options:

Grid File.

Soil depth (and soil bottom altitude, the effective grid needed) can be defined with a constant depth or estimated from slope HOW TO SoilBottom LINK.

Define the grid just generated, in the porous media data file with:

BOTTOM_FILE  : ..\..\GeneralData\PorousMedia\BottomLevel.dat

Water Level

Options:

Grid File.

The water table altitude represents the initial altitude of the water table. It is recommended to do a spin-up run to estabilize water level and then do a continuous simulation starting with the final water table achieved. Use the following blocks with Module FillMatrix standards:

<beginwaterlevel>
NAME                      : waterlevel
INITIALIZATION_METHOD     : ASCII_FILE
DEFAULTVALUE              : 0
REMAIN_CONSTANT           : 0
FILENAME                  : ..\..\GeneralData\PorousMedia\WaterLevel0.50.dat
<endwaterlevel>

Impermeability

Impermeability values (0 - completely permeable, 1 - impermeable) must be provided.

Options:

Constant Value.
Grid File. One possible option is to associate with land use shape file. In this case can use MOHID GIS going to menu [Tools]->[Shape to Grid Data] and provide: i) the grid (model grid), ii) the land use shape file and iii) the corespondence between land use codes and Impermeability values.

Use the following blocks with Module FillMatrix standards:

<beginimpermeablefraction>
NAME                      : impermeablefraction
INITIALIZATION_METHOD     : ASCII_FILE
DEFAULTVALUE              : 0
REMAIN_CONSTANT           : 1
FILENAME                  : ..\..\GeneralData\PorousMedia\AreaImpermeavel.dat
<endimpermeablefraction>

Outputs

Timeseries

Theta - is water content of selected cell (vol water/ vol soil)

relative_water_content - content in selected cell. between zero and one (zero is residual water content and one is saturated water content)

VelW_[m/s] - vertical velocity in the bottom face of the selected cell

VelW_Corr_[m/s] - vertical velocity in the bottom face of the selected cell that may be corrected if oversaturation occurs. if no correction occurs is the same as previous.

InF_Vel_[m/s] - infiltration velocity (in the soil surface)

Head_[m] - Suction in selected cell

Conductivity_[m/s] - Conductivity in selected cell

level_water_table_[m] - water table altitude

water_table_depth_[m] - water table depth (from soil surface)

Hydro_Pressure_[m] - hydrostatic pressure in selected cell

Final_Head_[m] - Soil water charge in selected cell

[Check Mohid Land Heights and Levels to understand some of the outputs]

GW_flow_to_river_total_[m3/s] - Ground water flow to river if it is a river point

Surface_Evaporation_Flux_[m3/s] - evaporation flux (in the soil surface)

Transpiration_Flux_[m3/s] - transpiration flux in selected cell

[Check Mohid Land Heights and Levels to understand the difference between level and height results | dd]

References

Jury,W.A.,Gardner,W.R.,Gardner,W.H., 1991,Soil Physics
Van Genuchten, M.T., A closed form equation for predicting the hydraulic conductivity of unsaturated soils
Wu,J.,Zhang, R., Gui,S.,1999, Modelling soil water movement with water uptake by roots, Plant and soil 215: 7-17
Marcel G.Schaap and Martinus Th. van Genuchten, A modified Maulem van Genuchten Formulation for Improved Description of Hydraulic Conductivity Near Saturation, 16 December 2005

Data File

Keywords

Keywords read in the Data File

Keyword                   : Data Type         Default     !Comment

BOTTOM_FILE               : char              -           !Path to Bottom Topography File
START_WITH_FIELD          : logical           1           !Sets Theta initial Field Capacity
CONTINUOUS                : logical           0           !Continues from previous run
STOP_ON_WRONG_DATE        : logical           1           !Stops if previous run end is different from actual
                                                          !Start
OUTPUT_TIME               : sec. sec. sec.    -           !Output Time
TIME_SERIE_LOCATION       : char              -           !Path to File which defines Time Series
CONTINUOUS_OUTPUT_FILE    : logical           1           !Writes "famous" iter.log
CONDUTIVITYFACE           : integer           1           !Way to interpolate conducivity face
                                                          !1 - Average, 2 - Maximum, 3 - Minimum, 4 - Weigthed
HORIZONTAL_K_FACTOR       : real              1.0         !Factor for Horizontal Conductivity = Kh / Kv
CUT_OFF_THETA_LOW         : real              1e-6        !Disables calculation when Theta is near ThetaR
CUT_OFF_THETA_HIGH        : real              1e-15       !Set Theta = ThetaS when Theta > ThetaS - CUT_OFF_THETA_HIGH
MIN_ITER                  : integer           2           !Number of iterations below which the DT is increased
MAX_ITER                  : integer           3           !Number of iterations above which the DT is decreased
LIMIT_ITER                : integer           50          !Number of iterations of a time step (for restart)
THETA_TOLERANCE           : real              0.001       !Converge Parameter
INCREASE_DT               : real              1.25        !Increase of DT when iter < MIN_ITER
DECREASE_DT               : real              0.70        !Decrease of DT when iter > MAX_ITER

<beginproperty>
NAME                      : Theta / waterlevel 

see Module FillMatrix for more options

<endproperty>

Sample

Some keywords of the PorousMedia input file:

BOTTOM_FILE               : ..\General Data\Other\PorousMedia\SoilBottom_2cells.dat
TIME_SERIE_LOCATION       : ..\General Data\TimeSeries\TimeSeriesLocation3D_2m.dat

COMPUTE_SOIL_FIELD        : 1 

OUTPUT_TIME               : 0 86400
CUT_OFF_THETA_HIGH        : 1e-15
START_WITH_FIELD          : 1

LIMIT_EVAP_WATER_VEL      : 0
LIMIT_EVAP_HEAD           : 0
HEAD_LIMIT                : -100
THETA_HYDRO_COEF          : 0.98


<beginsoiltype>
ID                        : 1
THETA_S                   : 0.43
THETA_R                   : 0.078
SAT_K                     : 2.888e-6
N_FIT                     : 1.56
ALPHA                     : 3.6
L_FIT                     : 0.50
<endsoiltype>


!----- Hydraulic Soil Properties
<beginhorizon>
KLB                       : 1
KUB                       : 10

<beginproperty>
NAME                      : SoilID
INITIALIZATION_METHOD     : CONSTANT
DEFAULTVALUE              : 1
<endproperty>

<beginproperty>
NAME                      : Theta
INITIALIZATION_METHOD     : CONSTANT
DEFAULTVALUE              : 0.30
<endproperty>
<endhorizon>


<beginwaterlevel>
NAME                      : waterlevel
INITIALIZATION_METHOD     : ASCII_FILE
DEFAULTVALUE              : 1.
REMAIN_CONSTANT           : 1
FILENAME                  : ..\General Data\Initial Conditions\InitialWaterLevel_2cells.dat
<endwaterlevel>

<beginimpermeablefraction>
NAME                      : impermeablefraction
INITIALIZATION_METHOD     : ASCII_FILE
DEFAULTVALUE              : 0
REMAIN_CONSTANT           : 1
FILENAME                  : ..\General Data\Other\PorousMedia\InitialImpermeabilization_2cells.dat
<endimpermeablefraction>

Personal tools

Difference between revisions of "Module PorousMedia" - MohidWiki

Search

Navigation

Tools

Difference between revisions of "Module PorousMedia"

From MohidWiki

Revision as of 17:23, 14 October 2011

Contents

Overview

Main Processes

Porous Media Geometry

Water Flow

Vadose Zone

Water content

Initial Condition

Water retention

Saturated and Unsaturated Conductivity

Evapotranspiration

Iteration Process

Other Features

How to Generate Info needed in Porous Media

SoilMap

Soil Bottom

Water Level

Impermeability

Outputs

Timeseries

References

Data File

Keywords

Sample

@@ Line 416: / Line 416: @@
 Transpiration_Flux_[m3/s] - transpiration flux in selected cell
-Check Mohid Land Heights and Levels to understand the difference between level and height results
+[Check Mohid Land Heights and Levels to understand the difference between level and height results | dd]
 ==References ==