Module PorousMedia
From MohidWiki
Contents
Overview
Module Porous Media is based on the Finite Volume Method in order to take in account the non-linear behavior of the soil. This module allows the calculation of the water fluxes in a porous media; in particular the infiltration flow is obtained from the potential water column available for this process. The potential water column is given by the Module Basin as reported below:
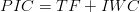
where:
PIC is the Potential Infiltration column (m) TF Throughfall is the percentage of the rain that reaches the soil (m) IWC is the Initial Water column (m)
The infiltration flows is calculated by the Buckingham-Darcy equation (Jury et al,1991)
Main Processes
Water flow
Soil contains a large distribution of pore sizes and channels through which water may flow. In general the water flow determination is based on the mass conservation and momentum equation. In the case of soil it is assumed that the forces of inertia are almost zero; therefore the balance is reduced to the forces of pressure, gravity and viscous. The equation that describes the flow through soil is the Buckingham Darcy equation (Jury et al,1991).
Failed to parse (Cannot write to or create math temp directory): J=-K\left ( \theta \right )\left ( \frac{\partial H}{\partial z} \right )=-K\left ( \theta \right )\left ( \frac{\partial h}{\partial z} + 1 \right )\,\,\,\,(1.1)\\
where:
J is the water velocity at the cell interface (m/s) H is the hydraulic head (m) θ is the water content (m3/m3) K is the hydraulic conductivity (m/s)
In particular the hydraulic head is given by the formula:
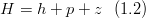
where:
h is the hydraulic head (m) p is hydrostatic pressure (m) z is the topography (m)
The soil is a very complex system, made up of a heterogeneous mixture of solid, liquid, and gaseous material. The liquid phase consists of soil water, which fills part or all of the open spaces between the soil particles. Therefore it is possible to divided the soil in two layers:
- Saturated soil
 The soil pores are filled by water
The soil pores are filled by water
- Unsaturated one
 The soil pores are filled by water and air
The soil pores are filled by water and air
In the first case the equation of Buckingham Darcy is simplified to the Darcy law and the parameter associated for its resolution are connected with the saturated layer. On the other hand for the resolution of the equation (1.1) a description of the characteristics of the the unsaturated layer is needed.
Vadose Zone
Many vadose flow and transport studies require description if unsaturated soil hydraulic proprieties over a wide range of pressure head. The hydraulic proprieties are described using the porous size distribution model of Maulem (1976) for hydraulic conductivity in combination with a water retention function introduced by Van Genuchten (1980).
Water content
Water content is the quantity of water contained in the soil (called soil moisture). It is given as a volumetric basis and it is defined mathematically as:
- Failed to parse (Cannot write to or create math temp directory): \theta = \frac{V_w}{V_T}\hspace{5cm}(1.3)
- Failed to parse (Cannot write to or create math temp directory): V_T = V_s + V_v = V_s + V_w + V_a\hspace{1.6cm}(1.4)
where:
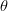
is water content (m 3/m 3) 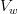
is the volume of water (m s3) 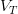
is the total volume (m 3) 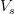
is the soil volume (m 3) 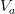
is the air space (m 3)
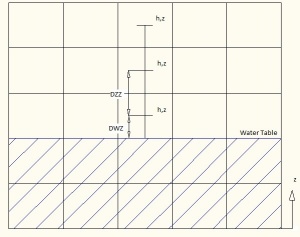
Once determined the aquifer level (water table) the water content is associated at each cells by the following criteria:
- If the cell is located above the water table
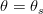
- If the cell is located over the water table
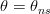
- If the cell is located above the water table
where:
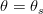
is the water content in the saturated soil (m3/m3) 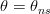
is the water content in the non saturated soil (m3/m3)
The water content in the non saturated soil can be associated with observed data, if these are not available it is imposed by default the water content equal to the Field Capacity. In order to calculate this parameter by the equation (1.7) the evaluation of the suction head is needed :
- Failed to parse (Cannot write to or create math temp directory): h=-DWZ\cdot 0.5\hspace{2cm}for\,\, the\,\, cells\,\, immediately\,\, above\,\, the\,\, water\,\, table \hspace{5cm} (1.5)
- Failed to parse (Cannot write to or create math temp directory): h=-(-DZZ-h)\hspace{1.5cm}for\,\, the\,\, other\,\, cells\hspace{9.75cm} (1.6)
As shown in the picture the suction head is calculated in order to maintain the same total head (H=z+p+h) in the cells in agreement with the field capacity definition.
Water retention
The model use for characterizing the shape of water retention curves is the van Genuchten model:
- Failed to parse (Cannot write to or create math temp directory): \theta(h) = \theta_r + \frac{\theta_s - \theta_r}{\left[ 1+(\alpha |h|)^n \right]^{1-1/n}}\hspace{0.5cm}\Longrightarrow\hspace{0.5cm}h(\theta)=\left |\frac{(S_{E}^{-1/n}-1)^{1/n}}{\alpha} \right |\hspace{3cm}(1.7)
- Failed to parse (Cannot write to or create math temp directory): S_{E}=\frac{\theta-\theta_{r}}{\theta_{s}-\theta_{r}}\hspace{11cm}(1.8)
where:
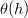
is the the water retention curve (m 3/m 3) 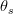
is the saturated water content (m 3/m 3) 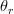
is the residual water content (m 3/m 3) h is the suction head (m) 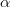
is related to the inverse of the air entry (m -1) n is a measure of the pore-size distribution n>1 (dimensionless) 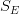
is the effective saturation (dimensionless)
Saturated and Unsaturated Conductivity
The saturated conductivity is given depending on the type of soil; instead the unsaturated conductivity is obtained from the suction head by the Maulem model:
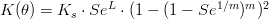
where:
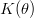
is the unsaturated conductivity (m/s) 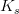
is the saturated conductivity(m/s) L empirical pore-connectivity (m) m m=1-1/n(dimensionless)
Evapotranspiration
Some water may disappear from the soil because of the evaporation and transpiration processes, which become a sink in soil water profile. These two processes, currently named Evapotranspiration may be modeled using the Penmann Monteith equation.

- λv = Latent heat of vaporization. Energy required per unit mass of water vaporized. (J/g)
- Lv = Volumetric latent heat of vaporization. Energy required per water volume vaporized. (Lv = 2453 MJ m-3)
- E = Mass water evapotranspiration rate (g s-1 m-2)
- ETo = Water volume evapotranspired (m3 s-1 m-2)
- Δ = Rate of change of saturation specific humidity with air temperature. (Pa K-1)
- Rn = Net irradiance (W m-2), the external source of energy flux
- cp = Specific heat capacity of air (J kg-1 K-1)
- ρa = dry air density (kg m-3)
- δe = vapor pressure deficit, or specific humidity (Pa)
- ga = Hydraulic conductivity of air, atmospheric conductance (m s-1)
- gs = Conductivity of stoma, surface conductance (m s-1)
- γ = Psychrometric constant (γ ≈ 66 Pa K-1)
All of these calculations about potential evapotranspiration are made in module Basin in MohiLand model. However, not all of the potential water that can be evaporated or transpirated will be in fact removed from the soil. The water that will really leave the soil through these processes is calculated in the Porous Media module. In Figure below it can be seen that the actual transpiration and evaporation are calculated in Porous Media module of MohidLand. The actual evaporation, which happens only at the soil surface, is calculated based on a pressure head limit imposed by the user. It allows the model to not evaporate any surface water, even if it is available, when the soil is very far way from the saturation point.
Iteration Process
Once obtained the water fluxes a balance on the water volume of each cell is apply in order to obtain the new water content 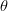 . The balance applied is the following:
. The balance applied is the following:
Horrizontal Direction X
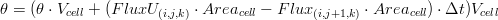
Horrizontal Direction Y
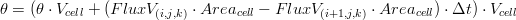
Vertical Direction W
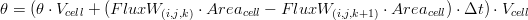
Transpiration Flux
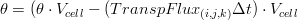
Evaporation Flux
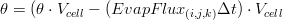
Infiltration Flux
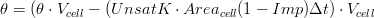
where:
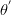
is the water content of the previous iteration (m 3/m 3)
The value of 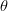 so obtained is compared with one used in the volumes calculation and the iterative process stop when:
so obtained is compared with one used in the volumes calculation and the iterative process stop when:
Failed to parse (Cannot write to or create math temp directory): (\theta^{'})-(\theta^{new})<\,\, Tolerance\hspace{3cm} (1.9)
where:
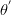
is the water content of the previous iteration (m 3/m 3)
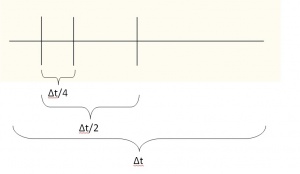
If the equation (1.9) is not satisfy the temporal step is divided in half and the new value of 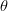 is used for solving the equation (1.7) for restarting the calculation process. The iteration process is stoped when the tolerance desired is reached.
is used for solving the equation (1.7) for restarting the calculation process. The iteration process is stoped when the tolerance desired is reached.
Other Features
How to Generate Info needed in Porous Media
SoilMap
Model needs to know soil ID in each cell and layer to pick hydraulic properties from that type of soil.
Options:
- Constant value
- Soil Grid. One possible option is to associate with soil shape file. In this case can use MOHID GIS going to menu [Tools]->[Shape to Grid Data] and provide: i) the grid (model grid), ii) the soil shape file and iii) the corespondence between soil codes and soil ID defined in data file.
Soil ID must be defined in Module FillMatrix standards for each soil horizon defined (grid example):
<beginhorizon> KLB : 1 KUB : 10
<beginproperty> NAME : SoilID DEFAULTVALUE : 1 INITIALIZATION_METHOD : ASCII_FILE REMAIN_CONSTANT : 1 FILENAME : ..\..\GeneralData\PorousMedia\SoilID200m.dat <endproperty> <beginproperty> <endproperty> .. <endhorizon>
Remarks
All the soil ID's appearing in the soil grid(s) must be defined in the PorousMedia data file in terms of hydraulic properties:
<beginsoiltype> ID : 1 THETA_S : 0.3859 THETA_R : 0.0476 N_FIT : 1.39 SAT_K : 3.5556e-6 ALPHA : 2.75 L_FIT : 0.50 THETA_CV_MIN : 0.2844 THETA_CV_MAX : 0.3791 <endsoiltype> <beginsoiltype> ID : 2 ... <endsoiltype> ...
Soil Bottom
The soil depth must be known by the model. This is computed by the model from terrain altitude (topography) and soil bottom altitude. As so, a soil bottom grid is needed.
Options:
- Grid File.
Soil depth (and soil bottom altitude, the effective grid needed) can be defined with a constant depth or estimated from slope HOW TO SoilBottom LINK.
Define the grid just generated, in the porous media data file with:
BOTTOM_FILE : ..\..\GeneralData\PorousMedia\BottomLevel.dat
Water Level
Options:
- Grid File.
The water table altitude represents the initial altitude of the water table. It is recommended to do a spin-up run to estabilize water level and then do a continuous simulation starting with the final water table achieved. Use the following blocks with Module FillMatrix standards:
<beginwaterlevel> NAME : waterlevel INITIALIZATION_METHOD : ASCII_FILE DEFAULTVALUE : 0 REMAIN_CONSTANT : 0 FILENAME : ..\..\GeneralData\PorousMedia\WaterLevel0.50.dat <endwaterlevel>
Impermeability
Impermeability values (0 - completely permeable, 1 - impermeable) must be provided.
Options:
- Constant Value.
- Grid File. One possible option is to associate with land use shape file. In this case can use MOHID GIS going to menu [Tools]->[Shape to Grid Data] and provide: i) the grid (model grid), ii) the land use shape file and iii) the corespondence between land use codes and Impermeability values.
Use the following blocks with Module FillMatrix standards:
<beginimpermeablefraction> NAME : impermeablefraction INITIALIZATION_METHOD : ASCII_FILE DEFAULTVALUE : 0 REMAIN_CONSTANT : 1 FILENAME : ..\..\GeneralData\PorousMedia\AreaImpermeavel.dat <endimpermeablefraction>
Outputs
References
- Jury,W.A.,Gardner,W.R.,Gardner,W.H., 1991,Soil Physics
- Van Genuchten, M.T., A closed form equation for predicting the hydraulic conductivity of unsaturated soils
- Wu,J.,Zhang, R., Gui,S.,1999, Modelling soil water movement with water uptake by roots, Plant and soil 215: 7-17
- Marcel G.Schaap and Martinus Th. van Genuchten, A modified Maulem van Genuchten Formulation for Improved Description of Hydraulic Conductivity Near Saturation, 16 December 2005
Data File
Keywords
Keywords read in the Data File
Keyword : Data Type Default !Comment
BOTTOM_FILE : char - !Path to Bottom Topography File
START_WITH_FIELD : logical 1 !Sets Theta initial Field Capacity
CONTINUOUS : logical 0 !Continues from previous run
STOP_ON_WRONG_DATE : logical 1 !Stops if previous run end is different from actual
!Start
OUTPUT_TIME : sec. sec. sec. - !Output Time
TIME_SERIE_LOCATION : char - !Path to File which defines Time Series
CONTINUOUS_OUTPUT_FILE : logical 1 !Writes "famous" iter.log
CONDUTIVITYFACE : integer 1 !Way to interpolate conducivity face
!1 - Average, 2 - Maximum, 3 - Minimum, 4 - Weigthed
HORIZONTAL_K_FACTOR : real 1.0 !Factor for Horizontal Conductivity = Kh / Kv
CUT_OFF_THETA_LOW : real 1e-6 !Disables calculation when Theta is near ThetaR
CUT_OFF_THETA_HIGH : real 1e-15 !Set Theta = ThetaS when Theta > ThetaS - CUT_OFF_THETA_HIGH
MIN_ITER : integer 2 !Number of iterations below which the DT is increased
MAX_ITER : integer 3 !Number of iterations above which the DT is decreased
LIMIT_ITER : integer 50 !Number of iterations of a time step (for restart)
THETA_TOLERANCE : real 0.001 !Converge Parameter
INCREASE_DT : real 1.25 !Increase of DT when iter < MIN_ITER
DECREASE_DT : real 0.70 !Decrease of DT when iter > MAX_ITER
<beginproperty>
NAME : Theta / waterlevel
see Module FillMatrix for more options
<endproperty>
Sample
Some keywords of the PorousMedia input file:
<beginsoiltype> *Saturated water content THETA_S : 0.55 *residual water content THETA_R : 0.1 *N of Van Genuchten: 1.5(clay) to 4.5 (sandy) N_FIT : 1.15 *Saturated hydraulic conductivity SAT_K : 1.39e-8 *alpha of Van Genuchten: 0.005 (clay) - 0.035 (sandy) ALPHA : 0.02 *L of Mualem - Van Genuchten (mostly 0.5) L_FIT : 0.50 <endsoiltype>