Module Runoff

Overview

Module Runoff allows the calculation of the overland surface runoff over a regular structured grid as function of the water column and terrain slope. The water column, namely the water located above the terrain, is given by the Module Basin after considering the precipitation input and the losses due to the evaporation and the infiltration. Overland flow is evaluated by the Manning’s equation.

Main Processes

Manning Equation

The overland surface runoff flow (m3/s) is calculated at the cell faces and it is obtained by applying the Manning's equation <ref>Gauckler, P. (1867), Etudes Théoriques et Pratiques sur l'Ecoulement et le Mouvement des Eaux, Comptes Rendues de l'Académie des Sciences, Paris, France, Tome 64, pp. 818–822</ref> :

Failed to parse (Cannot write to or create math temp directory): Q=\frac{1}{n}\cdot A\cdot R_{h}^{2/3}\cdot s^{1/2}\hspace {5.7cm}(1.1)

where:

Q	is the overland flow (m3/s)
A	is the area of the cross-section (m2)
n	is the Manning coefficient (s/m1/3)
Rh	is the hydraulic radius (m)
S	is the slope of the water surface (m/m)

In order to apply the Manning's equation each grid cell is considered as an open channel as shown in the scheme below.

Figure 1: Cell scheme

where:

h	is the water column (m)
w	is the cell width (m)

Hydraulics radius

In channels, the hydraulic radius is evaluated by the formula:

Failed to parse (Cannot write to or create math temp directory): \[R_{h}=\frac{w\cdot h}{w+2\cdot h}\hspace {6.8cm}(1.2)

But in runoff the lateral cell face is open boundary (to the next cell) not exerting fricition in a surface, and so hydraulic radius can be rewritten:

Failed to parse (Cannot write to or create math temp directory): \[R_{h}=\frac{w\cdot h}{w}\hspace {6.8cm}(1.2)

and the hydraulic radius is R_h=h. Therefore the Manning's equation can be rewritten as:

Failed to parse (Cannot write to or create math temp directory): \[Q=\frac{1}{n}\cdot w\cdot h^{5/3}\cdot s^{1/2}\hspace {5.8cm}(1.3)

Slope

The slope (s) is calculated by the difference of the water levels at the extremities of the considered cell:

Failed to parse (Cannot write to or create math temp directory): \[H(i,j)=\h(i,j)+T(i,j)\hspace {5.5cm}(1.4)

where:

H	is the water level (m)
h(i,j)	is the water column (m)
T(i,j)	is the Topography (m)
j	is X direction
i	is Y direction

Failed to parse (Cannot write to or create math temp directory): \[s_{x}=\frac{H(i,j-1)-H(i,j)}{DZX}\hspace {5.1cm}(1.5)

where:

sx	is the slope in the X direction (m)
H(i,j-1)	is the water column at the left face of the cell (m)
H(i,j)	is the water column at the right face of the cell (m)
DZX	is width of the cell in the X direction (m)

Failed to parse (Cannot write to or create math temp directory): \[s_{y}=\frac{H(i-1,j)-H(i,j)}{DZY}\hspace {5.1cm}(1.6)

where:

sy	is the slope in the Y direction (m)
H(i-1,j)	is the water column at the left face of the cell (m)
H(i,j)	is the water column at the right face of the cell (m)
DZY	is width of the cell in the X direction (m)

In order to take in account the limitation given by the Manning's equation (1.1)[it tends to overestimate the flow velocity when solpe > 0.04] , the slope value obtained by the formulas (1.5) and (1.6) it is subsequently adjusted by the following function:

Failed to parse (Cannot write to or create math temp directory): s= 0.05247 + 0.06363 \cdot s - 0.182\cdot e^{(-62.38\cdot s)}\hspace {2.4cm}(1.7)

where:

s	is the slope (m)

Manning cofficient

The Manning coefficient is derived from the land use map. Indeed by using a GIS program it is possible to associate at each cell a land use class in order to obtain, by the support of an abacus or table, a Manning coefficent value.

Calculated Flows

The flows obtained by the equation (1.3) are diveded into flows in X direction and Y direction according with the Figure 2.

Figure 2:Flow directions

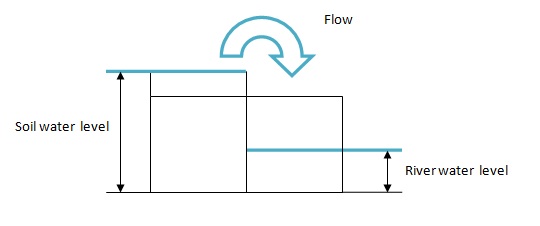
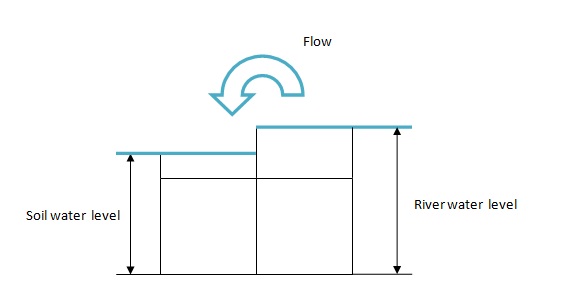
In the eventuality presence of a river in the basin analyzed it is possible to obtain two different configurations:

• Flow to the river when the water level of the river is lower that soil one

Figure 3: Flow to the river

• Flow from the river when the water level is higher than the soil one

Figure 4: Flow from the river

The flow between river and runoff is computed using the same formulation as in runoff cells using the surface gradient between runoff and river.

Other Features

How To Generate Manning Coefficients

Manning coefficients must be provided in runoff data file.

Options:

• Use a constant value
• Define a Manning's grid: One possible option is to associate Manning with land use classes (shape file). In this case can use MOHID GIS going to menu [Tools] $\Longrightarrow$ [Shape to Grid Data] and provide:

(i) the grid (model grid)

ii) the land use shape file

iii) the corespondence between land use codes and Manning

Use Manning inicialization with Module FillMatrix standards in the block:

<BeginOverLandCoefficient>
FILE_IN_TIME           : NONE
INITIALIZATION_METHOD  : ASCII_FILE
REMAIN_CONSTANT        : 1
DEFAULTVALUE           : 0.08
FILENAME               : ..\..\GeneralData\Runoff\Mannings200m_v2.dat 
<EndOverLandCoefficient>

References

• Hubert Chanson|Chanson, H. (2004), The Hydraulics of Open Channel Flow, Butterworth-Heinemann, Oxford, UK, 2nd edition, 630 pages
• http://www.hkh-friend.net.np/rhdc/training/lectures/HEGGEN/Tc_3.pdf