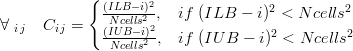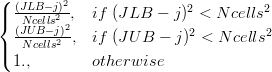Difference between revisions of "SmoothBatimCoefs"

Latest revision as of 17:53, 1 August 2011

This program creates smoothing coefficients for a bathimetry to allow a smooth transition in the boundary between the the bathymetry and a larger scale one. See also SmoothBatimNesting.

Quick start

Create the son bathymetry (you may use Mohid GIS).
Create and edit the options SmoothBatimCoef.dat file and save it in the same path as the executable.
Run the executable.

Options file

Here's what the options file SmoothBatimCoef.dat looks like:

SON_BATIM                   : ..\GridData_2.dat
NEW_COEF                    : SmoothCoefs.dat
NUMBER_CELLS                : 10

The Number_cells are the number of grid points taken from the border in, that will yield non-null smoothing coefficients.

Algorithms

So far there is only one type of algorithm for the smoothing coefficient 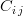$C_{i\,j}$ defined here. It's basically a quadratic growth from 0 to 1 from the border to Ncells inside, where Ncells is a parameter given by the modeller. Here's the formula:

ILB: lower bound in the i direction.
IUB: upper bound in the i direction.
JLB: lower bound in the j direction.
JUB: upper bound in the j direction.

\forall\;_{i\,j}\quad C_{i\,j} = \begin{cases} \frac{(ILB-i)^2}{Ncells^2}, & if\; (ILB-i)^2 < Ncells^2 \\ \frac{(IUB-i)^2}{Ncells^2}, & if\; (IUB-i)^2 < Ncells^2\end{cases}

\begin{cases} \frac{(JLB-j)^2}{Ncells^2}, & if\; (JLB-j)^2 < Ncells^2 \\ \frac{(JUB-j)^2}{Ncells^2}, & if\; (JUB-j)^2 < Ncells^2 \\ 1., & otherwise \end{cases}

Future algorithms

Please place here the algorithms you'd wish be implemented:

...

@@ Line 22: / Line 22: @@
 *''JUB'': upper bound in the ''j'' direction.
-:<math>\forall\;_{i\,j}\quad C_{i\,j} = \begin{cases} \frac{(ILB-i)^2}{Ncells^2}, & \mbox{if}\; (ILB-i)^2 < Ncells^2 \\ \frac{(IUB-i)^2}{Ncells^2}, & \mbox{if}\; (IUB-i)^2 < Ncells^2 \\ \frac{(JLB-j)^2}{Ncells^2}, & \mbox{if}\; (JLB-j)^2 < Ncells^2 \\ \frac{(JUB-j)^2}{Ncells^2}, & \mbox{if}\; (JUB-j)^2 < Ncells^2 \\ 1., & \mbox{otherwise} \end{cases}</math>
+:<math>\forall\;_{i\,j}\quad C_{i\,j} = \begin{cases} \frac{(ILB-i)^2}{Ncells^2}, & if\; (ILB-i)^2 < Ncells^2 \\ \frac{(IUB-i)^2}{Ncells^2}, & if\; (IUB-i)^2 < Ncells^2\end{cases}</math>
+:<math> \begin{cases} \frac{(JLB-j)^2}{Ncells^2}, & if\; (JLB-j)^2 < Ncells^2 \\ \frac{(JUB-j)^2}{Ncells^2}, & if\; (JUB-j)^2 < Ncells^2 \\ 1., & otherwise \end{cases}</math>
 ===Future algorithms===
 Please place here the algorithms you'd wish be implemented:
 *...

Personal tools

Difference between revisions of "SmoothBatimCoefs" - MohidWiki

Search

Navigation

Tools