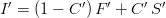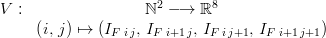SmoothBatimNesting
From MohidWiki
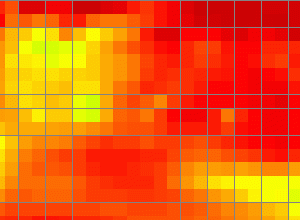
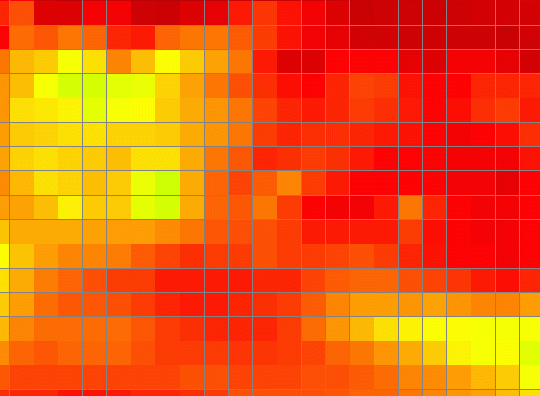
This program creates a new sub-model bathimetry to allow a smooth transition in the boundary between the coarser model and the high resolution model. See also SmoothBatimCoefs.
Quick start
- Create the father and son bathymetries (you may use Mohid GIS).
- Create the SmoothCoeficients griddata file (you may use SmoothBatimCoefs).
- Create and edit the options SmoothBatimNesting.dat file and save it in the same path as the executable.
- Run the executable.
Options file
Here's what the options file SmoothBatimNesting.dat looks like:
FATHER_BATIM : ..\..\WestIberiaTide\GridData.dat SON_BATIM : ..\GridData_2.dat SMOOTH_COEF : SmoothCoef.dat NEW_SON_BATIM : SmoothData.dat
Smoothing algorithm
Let it be 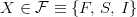 , as an element of the father, the son and the interpolated bathymetries discrete fields. Let it be
, as an element of the father, the son and the interpolated bathymetries discrete fields. Let it be 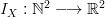 as the respective index mapping function. Let it be
as the respective index mapping function. Let it be 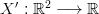 , a continuous map, so that
, a continuous map, so that 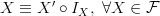 . Let
. Let 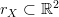 define the work domain of
define the work domain of 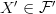 . In particular,
. In particular, 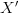 verifies
verifies 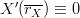 . The son grid is the same as the interpolated grid, meaning
. The son grid is the same as the interpolated grid, meaning 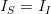 . However, the father field is completely independent from the other fields, meaning that
. However, the father field is completely independent from the other fields, meaning that 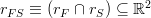 . The smoothing algorithm is a simple linear interpolation of the father and son fields:
. The smoothing algorithm is a simple linear interpolation of the father and son fields:
where the smoothing coefficient is given by ![C^\prime: \mathbb{R}^2 \longrightarrow \left[0\;1\right]](/images/math/3/6/9/369d5cf0d68b7852eb9f308576a33a4d.png) . Thus, the smoothing coefficient gridded counterpart
. Thus, the smoothing coefficient gridded counterpart 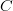 is defined; and its index mapping function
is defined; and its index mapping function 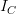 is equal to the son's; meaning
is equal to the son's; meaning 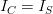 . Let us define the grid
. Let us define the grid 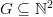 such that
such that 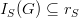 and
and 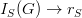 . Thus the smoothing coefficient
. Thus the smoothing coefficient 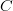 needs can be defined in
needs can be defined in 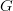 . Concretely speaking,
. Concretely speaking, 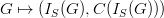 is the smoothing coefficient's Grid Data file described above, thus it leaves to the modeller the choice of the smoothing coefficient field.
is the smoothing coefficient's Grid Data file described above, thus it leaves to the modeller the choice of the smoothing coefficient field.
Implementation
Let us define a collection of four-vertices polygons taken from the father grid:
where 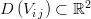 is the subdomain defined by the vertices of
is the subdomain defined by the vertices of 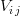 .
Let us define an auxiliary grid of the son grid given by:
.
Let us define an auxiliary grid of the son grid given by:
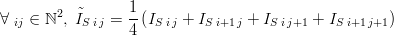 .
.
Let us define a new mapping into a subset of 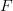 's image:
's image:
- \
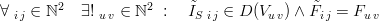 .
.
Here's the implemented smoothing algorithm:
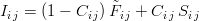 .
.