Lagged correlation
From MohidWiki
Convolution or cross-correlation are similar operands that can be applied to any square-integrable real functions 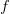 and
and 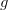 .
.
Contents
Convolution
-
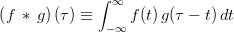 .
.
Cross-correlation
-
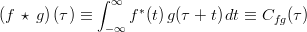 .
.
- In particular
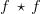 is designated the autocorrelation.
is designated the autocorrelation.
Normalized
- Failed to parse (Cannot write to or create math temp directory): \widehat{C}_{fg}(\tau) \equiv \frac{\int_{-\infty}^{\infty} F^{*}(t) \, G(\tau+t) \,dt}{\int_{-\infty}^{\infty} F^{*}(t) \, F(t) \,dt \, \int_{-\infty}^{\infty} G^{*}(t) \, G(t) \,dt} = \left< \frac{F(t)}{\|F\|} ,\, \frac{G(\tau+t)}{\|G\|} \right>
, where
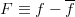 . The idea is to remove the average and, optionally, other linear or physical trends from
. The idea is to remove the average and, optionally, other linear or physical trends from 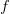 .
.
- In particular we have
- Failed to parse (Cannot write to or create math temp directory): \widehat{C}_{fg}(0) = \left< \frac{F}{\|F\|} ,\, \frac{G}{\|G\|} \right> .
-
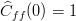 .
.
Discretized
-
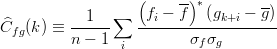 , where
, where 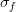 is the variance of
is the variance of 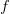 .
.
- In particular
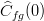 is the famous correlation coefficient.
is the famous correlation coefficient.
Example
When both 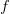 and
and 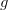 are even functions then the convolution and cross-correlation products are rigorously equivalent. Below, we show these products when applied to box functions (left figure) and to gaussian functions (right figure). In both cases, they are even functions.
are even functions then the convolution and cross-correlation products are rigorously equivalent. Below, we show these products when applied to box functions (left figure) and to gaussian functions (right figure). In both cases, they are even functions. 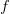 is represented by the red line,
is represented by the red line, 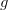 is represented by the blue line, the product
is represented by the blue line, the product 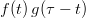 is represented by the solid blue line. The solid blue area is the convolution product for lag-time
is represented by the solid blue line. The solid blue area is the convolution product for lag-time  and the whole convolution product function (for all
and the whole convolution product function (for all  ) is represented by the green line.
) is represented by the green line.
http://mathworld.wolfram.com/images/gifs/convrect.gif http://mathworld.wolfram.com/images/gifs/convgaus.gif
The big conclusions we can make is that if 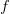 and
and 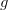 are the same functions, but with a lag of
are the same functions, but with a lag of  between them, then the cross-correlation product is maximum when
between them, then the cross-correlation product is maximum when  .
.
Matlab functions
xcorr
Calculates the cross correlation from two signals.
%Consider arrays t, y1(t), y2(t)
N=length(t);
tlag = linspace(-t(N/2), t(N/2), N+1);
crosscorr = xcorr( y1, y2, N/2, 'coeff');
plot(tlag,crosscorr); xlabel('Phase in time units');ylabel('coefficient');
cpsd
Calculates the cross power spectral density (PSD) function of signals 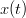 and
and 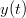 .
.
periodogram or pwelch
Calculates the power spectral density (PSD) function of signal 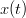 . The periodogram may use several window functions as option. The pwelch will use the welch window.
. The periodogram may use several window functions as option. The pwelch will use the welch window.
mscoherence
Calculates the coherence-squared spectrum function. If you apply an inverse Fourier transform (IFT), then you get the cross-correlation function in a very efficient way.