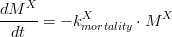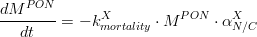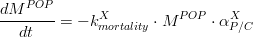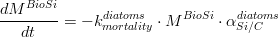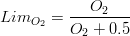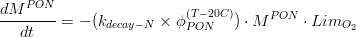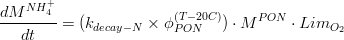Module Benthos

Overview

Module Benthos is a zero-dimensional biogeochemical model and was designed to compute, using simple model formulations, some of the main benthic biogeochemical processes occurring in an aquatic system: (i) Algae mortality, if algae are considered as a particulate property that can sink and deposit, then if deposited a mortality rate is applied; (ii) Particulate organic matter mineralization (nitrogen and phosphorus biogeochemical cycles); (iii) Biogenic silica dissolution; (iv) Oxygen depletion.

• algae mortality, if algae are considered as a particulate property that can sink and deposit, then if deposited a mortality rate is applied
• Particulate organic matter mineralization (nitrogen and phosphorus biogeochemical cycles)
• Biogenic silica dissolution
• Oxygen depletion

Module Benthos is also ready to be coupled, in terms of organic matter mineralization, biogenic silica dissolution and oxygen depletion, with other pelagic biogeochemical models included in Mohid such as: Module WaterQuality and Module Life.

Algae Mortality

A mortality rate can be applied over algae deposited in the water-sediment interface. ModuleBenthos is ready to assume phytoplankton and diatoms as algae.

As this happens, the algae nitrogen and phosphorus internal pools are converted into particulate organic matter, and for the specific case of diatoms, its silica pool is transformed into dissolved silica. Algae mortality is computed as described in (eq. 1).

$\frac{dM^{X}}{dt}= -k_{mortality}^{X} \cdot  M^{X}$

Where is the algae (phytoplankton or diatoms) deposited mass (kg of carbon), is the algae mortality rate (s-1).

Hence, the algae mortality generates an input for the particulate organic matter pool, which can be accounted in particulate organic nitrogen (PON), (eq.2) and particulate organic phosphorus (POP) (eq.3).

$\frac{dM^{PON}}{dt}= -k_{mortality}^{X} \cdot  M^{PON} \cdot \alpha_{N/C}^{X}$

Where is given in kg of Nitrogen and is the algae’s Nitrogen/Carbon ratio (which is different for phytoplankton and for diatoms).

$\frac{dM^{POP}}{dt}= -k_{mortality}^{X} \cdot  M^{POP} \cdot \alpha_{P/C}^{X}$

Where is given in kg of Phosphorus and is the algae’s Phosphorus/Carbon ratio (which is different for phytoplankton and for diatoms). For diatoms, the biogenic silica derived from its mortality, is computed as:

$\frac{dM^{BioSi}}{dt}= -k_{mortality}^{diatoms} \cdot  M^{BioSi} \cdot \alpha_{Si/C}^{diatoms}$

Where is given in kg of Silica and is the algae’s Silica/Carbon ratio (in the case of diatoms simulation).

Organic matter mineralization

Organic matter mineralization is computed over its nitrogen and phosphorus fractions, by means of a temperature dependent rate and considering that bacterial abundance is constant in time and its activity, as said, is temperature dependent. This mineralization process is responsible for oxygen depletion, but it’s also regulated by oxygen availability. If oxygen levels reach anoxia ( ) conditions then, organic matter mineralization is stopped. This limitation is computed as in (eq.5).

$Lim_{O_{2}}=\frac{O_{2}}{O_{2}+0.5}$

Thus for the nitrogen fraction of organic matter, mineralization can be computed as in (eq.6) and (eq.7), for PON and ammonia, respectively.

$\frac{dM^{PON}}{dt} = -(k_{decay-N} \times \phi_{PON}^{(T-20C)}) \cdot M^{PON} \cdot Lim_{O_{2}}$

$\frac{dM^{NH_{4}^{+}}}{dt}= (k_{decay-N} \times \phi_{PON}^{(T-20C)}) \cdot M^{PON} \cdot Lim_{O_{2}}$

Where is given in kg of Nitrogen, is the reference mineralization rate for PON, is a temperature coefficient, and is the water temperature at the water-sediment interface (ºC). Regarding the phosphorus budget: (eq.8)

(eq.9)

Where is given in kg of Phosphorus, is the reference mineralization rate for POP, is a temperature coefficient, and is the water temperature at the water-sediment interface (ºC). For more details on the oxygen budget, see chapter 2.4.

Silica dissolution

Silica dissolution is simulated as a constant rate over the biogenic silica deposited in the water-sediment interface, acting as a source of dissolved silica. (eq.10)

(eq.11)

Where is given in kg of biogenic silica, is given in kg of dissolved silica and is the dissolution rate for biogenic silica.

Oxygen depletion

Oxygen depletion occurs due to organic matter mineralization, and is computed according to stoichiometric relations. (eq.12)

(eq.13)

Where is given in kg of oxygen, and are the Nitrogen/Carbon and Phosphorus/Carbon ratios of particulate organic matter, and is the ratio between Oxygen and Carbon in CO2.

Numerical scheme

Module Benthos solves the differential equations described above using an Euler forward scheme (explicit method), which was used in order to make the code organization as simple as possible. When using this numerical method there are, nevertheless, some restraints in terms of temporal discretization, which can cause numerical instabilities that can be solved, at some extent, by using a smaller time step.

Module Benthos has an independent time step in relation to the model’s main time step. Normally the time step to integrate the differential equations describing these kind of biogeochemical reactions is much higher than the time step used to solve hydrodynamic and transport equations, and as the set of equations in this module is quite simple, there is no significant increase in terms of computational costs when using a smaller time step.

User guide

As described before, Module Benthos is directly connected with Module InterfaceSedimentWater, therefore making it necessary to understand some of the options to be made in the InterfaceSedimentWater input data file.

All properties undergoing biogeochemical reactions in Module Benthos must be defined in Module InterfaceSedimentWater, and keyword BENTHOS has to be activated in every one of it, including oxygen, which is mandatory to be computed.

BENTHOS	        : 1

Additionally, property temperature must be also defined, as it controls mineralization rates. Nevertheless, as temperature is not subject to any specific process in the bottom, the BENTHOS keyword value for this property must be set to 0.

Particulate properties, such as particulate organic nitrogen, particulate organic phosphorus, biogenic silica, phytoplankton (if desired) and diatoms (if desired) must be set as PARTICULATE.

PARTICULATE    : 1

Dissolved properties such as ammonia, inorganic phosphorus, dissolved silica, oxygen and temperature, must be set to PARTICULATE : 0.

The properties defined in the Module InterfaceSedimentWater must be consistent with the Module WaterProperties input file, which means that every property important for the benthic model must be defined in both input files;With exception to temperature, all dissolved properties defined in the Module InterfaceSedimentWater input file, with option BENTHOS activated, must set keyword WATER_FLUXES : 1. Particulate properties also need this option activated in order to compute the fluxes between the water column and the bottom due to erosion and deposition.

Also as Module Benthos computes biogeochemical processes involving dissolved processes near the sediment-water interface (e.g. oxygen depletion), all these properties must be defined in the water column. In addition, and as referred above, temperature, as it influences the mineralization rates, is mandatory to be defined in the Module WaterProperties input data file. With exception to temperature, all properties defined in the ModuleInterfaceSedimentWater input file with option BENTHOS activated, must set keyword to BOTTOM_FLUXES : 1 in the Module WaterProperties input file. This keywords activates an option that computes a bottom boundary condition in the transport equations of the dissolved properties due to the biogeochemical processes computed in Module Benthos.

For more on Module Benthos keywords go to MOHID keyword Database.

Useful notes

The results from ModuleBenthos are handled by Module InterfaceSedimentWater.