Upwelling
From MohidWiki
Upwelling is quite well described here.
Contents
Upwelling index
The upwelling index (UI) is defined as the Ekman Transport per 100 m of coastline induced by wind parallel to the coast. In the Western Iberian coast. This corresponds to the zonal component of the wind.
The volume Ekman transport is defined in Kundu as the momentum of a steady-state horizontally homogeneous viscid geophysical flow integrated over depth. Thus, assuming a steady state constant zonal wind stress 
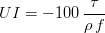 m3/s/100m.
m3/s/100m.
Wind stress
To calculate the wind stress  from the wind velocity modulus
from the wind velocity modulus 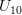 (air speed at 10 m height from the free surface) Ekman used the bulk formula:
(air speed at 10 m height from the free surface) Ekman used the bulk formula:
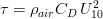
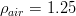 kg/m3 is an usual value for the air density.
kg/m3 is an usual value for the air density.
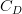 is an air drag coefficient. It is mainly dependent from surface rugosity length z0 and from the Richardson number. However a large case of linear parameterizations is available throughout the litterature, with no well defined standard:
is an air drag coefficient. It is mainly dependent from surface rugosity length z0 and from the Richardson number. However a large case of linear parameterizations is available throughout the litterature, with no well defined standard:

- Large & Pond 1981 use CD = .44 + .63 U10,
- Smith & Banke 1975 use CD = .63 + .66U10.
Viscid, horizontally homogeneous, steady-state, geophysical fluid equations
The flow equations of motion are given in Kundu by
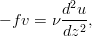
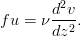
The Ekman spiral
Kundu shows that when acted by a constant wind stress  along the x-direction, the solution to the above equations yield
along the x-direction, the solution to the above equations yield
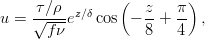
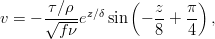
where 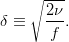
The velocity vector rotates clockwise (looking down) with dept. Its magnitude decays exponentially as well with decay constant  . This spiral shaped flow is called the Ekman spiral.
In the works of Ekman, Ekman defined a thickness of decay of the spiraled flow based on the flow geometry. This thickness later defined the Ekman layer and is usually around 50 m for the open ocean(Stewart). Kundu however defines the thickness of the Ekman layer simply by its decay constant
. This spiral shaped flow is called the Ekman spiral.
In the works of Ekman, Ekman defined a thickness of decay of the spiraled flow based on the flow geometry. This thickness later defined the Ekman layer and is usually around 50 m for the open ocean(Stewart). Kundu however defines the thickness of the Ekman layer simply by its decay constant  .
.
The Ekman transport
When acted by a constant wind stress  along the x-direction, the volume transport in the Ekman layer is given by
along the x-direction, the volume transport in the Ekman layer is given by
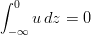 ,
,
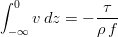 .
.
Thus the net transport is to the right of the wind stress in the northern hemisphere and is independent of viscosity. This is due because near the surface 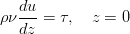 .
Over statistical flow averages, the Ekman transport calculation fits very well with experimental data and, thus, is considered a reliable calculation.
.
Over statistical flow averages, the Ekman transport calculation fits very well with experimental data and, thus, is considered a reliable calculation.
References
- Kundu
- Stewart
- Pietrzak2002
- Large & Pond 1981
- Smith & Banke 1975